题目内容
如图，一次函数y＝2x和y＝ax＋4的图像相交于点A(m，3)，则方程ax＋4＝0的解为( )
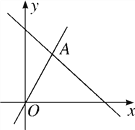
A. x＝6 B. x＝3 C. x＝－6 D. x＝－3
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
孟建平小学滚动测试系列答案黄冈天天练口算题卡系列答案题目内容
如图，一次函数y＝2x和y＝ax＋4的图像相交于点A(m，3)，则方程ax＋4＝0的解为( )
A. x＝6 B. x＝3 C. x＝－6 D. x＝－3
孟建平小学滚动测试系列答案黄冈天天练口算题卡系列答案
B. 
C. 
D. 
B. 
C. 
D. 
x＋3，下列说法：①函数图像经过点(2，2)；②y随着x的增大而减小；③函数图像与x轴的交点是(6，0)；④函数图像与坐标轴围成的三角形面积是9.其中正确的有( )
___________.
