Question

【题目】已知抛物线y=mx2的图像经过点（1,2）.

（1）求出m的值和顶点的坐标，并画出这条抛物线；

（2）利用图像回答：x取什么值时，抛物线在直线y=2的上方？

（3）当－1≤x≤2时，求y的取值范围.

Answer 1

【答案】(1)m=2 ，顶点（0,0）， 图象见解析；（2）x>1或x<-1；（3）.

【解析】

(1)由y=mx2的图像过点（1,2），可得m的值并画出图像；

（2）观察图像，可得x的取值范围；

(3)利用二次函数性质，可得当－1≤x≤2时，求y的取值范围.

解：（1）已知抛物线经y=mx2的图像过点（1,2），可得2=m1，

m=2， y=2x2

图像如图：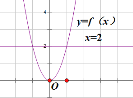

(2)由图像可知，当x>1或x<-1，抛物线在直线y=2的上方；

(3) 由图像可知，当x=0时，有最小值y=0；

当x=2时，有最大值,y=8;

当－1≤x≤2时,0≤y≤8.