题目内容
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.
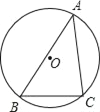
【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()
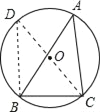
点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
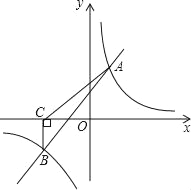
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.
【答案】(1)反比例函数的解析式是y=![]() ;一次函数的解析式是y=x+1;(2)﹣3<x<0或x>2;(3)p≤﹣2或p>0.
;一次函数的解析式是y=x+1;(2)﹣3<x<0或x>2;(3)p≤﹣2或p>0.
;
【解析】试题分析:(1)把A(2,m),B(n,2)代入反比例函数解析式求出m=n, 过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,根据三角形的面积公式可得出关于n的方程,求出n的值,得出![]() 的坐标,代入反比例函数和一次函数的解析式,即可求出答案;
的坐标,代入反比例函数和一次函数的解析式,即可求出答案;
(2)根据![]() 的横坐标,结合图象即可得出答案;
的横坐标,结合图象即可得出答案;
(3)分为两种情况:当点![]() 在第三象限时和当点
在第三象限时和当点![]() 在第一象限时,根据坐标和图象即可得出答案.
在第一象限时,根据坐标和图象即可得出答案.
试题解析:(1)把A(2,m),B(n,2)代入![]() 得:k2=2m=2n,
得:k2=2m=2n,
即m=n,
则A(2,n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
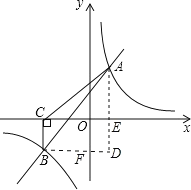
∵A(2,n),B(n,2),
∴BD=2n,AD=n+2,BC=|2|=2,
∵![]()
![]() 解得:n=3,
解得:n=3,
即A(2,3),B(3,2),
把A(2,3)代入![]() 得:
得:![]()
即反比例函数的解析式是![]()
把A(2,3),B(3,2)代入![]() 得:
得:![]()
解得:![]()
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(3,2),
∴不等式![]() 的解集是3<x<0或x>2;
的解集是3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使![]() ,实数p的取值范围是
,实数p的取值范围是![]() ,
,
当点P在第一象限时,要使![]() ,实数p的取值范围是P>0,
,实数p的取值范围是P>0,
即P的取值范围是![]() 或p>0.
或p>0.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】某股民上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元)(周六、周日休盘)
星期 | 一 | 二 | 三 | 四 | 五 |
每股 涨跌 | +4 | +4.5 | -1 | -1.5 | -4 |
(1)星期五收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知该股民买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,若该股民在星期五收盘前将全部股票卖出,他的收益情况如何?