题目内容
 如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则由这个扇形围成的圆锥的底面半径是
如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则由这个扇形围成的圆锥的底面半径是2
| ||
| 3 |
2
| ||
| 3 |
分析:要求以A为圆心在梯形内画出一个最大的扇形(图中阴影部分)的周长,需过点A作AE⊥BC于点E,根据切线的性质求得AE是扇形的半径,再利用直角梯形的性质和直角三角形的性质求得扇形的半径和圆心角度数,再利用弧长公式求得扇形的底面半径即可.
解答: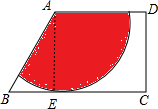 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,
∵AD∥BC,∠C=90°,
∴四边形ADCE是矩形,
∵AB=AD=4,BC=6,
∴CE=AD=4,BE=2
∴AE=2
,∠BAE=30°
∴∠BAD=90°+30°=120°
设底面半径为r,
则2πr=
解得:r=
故答案为:
 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,∵AD∥BC,∠C=90°,
∴四边形ADCE是矩形,
∵AB=AD=4,BC=6,
∴CE=AD=4,BE=2
∴AE=2
| 3 |
∴∠BAD=90°+30°=120°
设底面半径为r,
则2πr=
120π×2
| ||
| 180 |
解得:r=
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题要熟知切线的性质,直角梯形的性质和扇形弧长计算公式.利用切线的性质求得AE的长即半径是解题的关键,注意扇形的周长为两条半径的长加上弧长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.