题目内容
 (2013•百色)如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2.C2的图象与x轴交于A、B两点(点A在点B的左侧).
(2013•百色)如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2.C2的图象与x轴交于A、B两点(点A在点B的左侧).(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.
分析:(1)根据二次函数平移的规律:“左加右减,上加下减”,得出平移后解析式即可;
(2)首先求出A,B两点的坐标,再利用顶点坐标得出AC=CB,CE=CD,进而得出四边形ADBE是平行四边形以及四边形ADBE是菱形,再利用三角形面积公式求出即可;
(3)利用分OB为平行四边形的边和对角线两种情况:①当OB为平行四边形的一边时,②当OB为平行四边形的一对角线时分别得出即可.
(2)首先求出A,B两点的坐标,再利用顶点坐标得出AC=CB,CE=CD,进而得出四边形ADBE是平行四边形以及四边形ADBE是菱形,再利用三角形面积公式求出即可;
(3)利用分OB为平行四边形的边和对角线两种情况:①当OB为平行四边形的一边时,②当OB为平行四边形的一对角线时分别得出即可.
解答:解:(1)∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,-4).
∴抛物线C2的顶点坐标为(1,-4).
∴抛物线C2的解析式为y=(x-1)2-4,
即y=x2-2x-3;
(2)证明:由x2-2x-3=0,
解得:x1=-1,x2=3,
∵点A在点B的左侧,
∴A(-1,0),B(3,0),AB=4.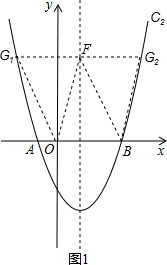
∵抛物线C2的对称轴为x=1,顶点坐标D为(1,-4),
∴CD=4.AC=CB=2.
将x=1代入y=x2+3得y=4,
∴E(1,4),CE=CD.
∴四边形ADBE是平行四边形.
∵ED⊥AB,
∴四边形ADBE是菱形.
S菱形ADBE=2×
×AB×CE=2×
×4×4=16.
(3)存在.分AB为平行四边形的边和对角线两种情况:
①当OB为平行四边形的一边时,如图1,
设F(1,y),
∵OB=3,∴G1(-2,y)或G2(4,y).
∵点G在y=x2-2x-3上,
∴将x=-2代入,得y=5;将x=4代入,得y=5.
∴G1(-2,5),G2(4,5).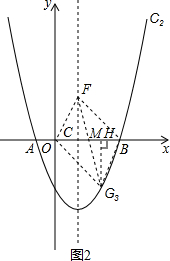
②当OB为平行四边形的一对角线时,如图2,
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM=
,CM=
.
∵△CFM≌△HGM(AAS),∴HM=CM=
.∴OH=2.
∴G3(2,-y).
∵点G在y=x2-2x-3上,
∴将(2,-y)代入,得-y=-3,即y=3.
∴G3(2,-3).
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(-2,5),G2(4,5),G3(2,-3).
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,-4).
∴抛物线C2的顶点坐标为(1,-4).
∴抛物线C2的解析式为y=(x-1)2-4,
即y=x2-2x-3;
(2)证明:由x2-2x-3=0,
解得:x1=-1,x2=3,
∵点A在点B的左侧,
∴A(-1,0),B(3,0),AB=4.

∵抛物线C2的对称轴为x=1,顶点坐标D为(1,-4),
∴CD=4.AC=CB=2.
将x=1代入y=x2+3得y=4,
∴E(1,4),CE=CD.
∴四边形ADBE是平行四边形.
∵ED⊥AB,
∴四边形ADBE是菱形.
S菱形ADBE=2×
| 1 |
| 2 |
| 1 |
| 2 |
(3)存在.分AB为平行四边形的边和对角线两种情况:
①当OB为平行四边形的一边时,如图1,
设F(1,y),
∵OB=3,∴G1(-2,y)或G2(4,y).
∵点G在y=x2-2x-3上,
∴将x=-2代入,得y=5;将x=4代入,得y=5.
∴G1(-2,5),G2(4,5).

②当OB为平行四边形的一对角线时,如图2,
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM=
| 3 |
| 2 |
| 1 |
| 2 |
∵△CFM≌△HGM(AAS),∴HM=CM=
| 1 |
| 2 |
∴G3(2,-y).
∵点G在y=x2-2x-3上,
∴将(2,-y)代入,得-y=-3,即y=3.
∴G3(2,-3).
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(-2,5),G2(4,5),G3(2,-3).
点评:此题主要考查了菱形的判定以及二次函数的平移和平行四边形的判定和性质等知识,利用分类讨论思想得出是解题关键.

练习册系列答案
相关题目
 (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2013•百色)如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为
(2013•百色)如图,在边长为10cm的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 (2013•百色)如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F.
(2013•百色)如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F. (2013•百色)如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与y=
(2013•百色)如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与y=