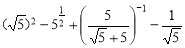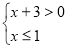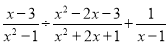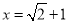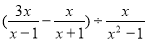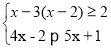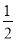Question

直线y=kx-6过点A（1，-4），与x轴交于点B，与y轴交于点D，以点A为顶点的抛物线经过点B，且交y轴于点C．

（1）求抛物线的表达式；

（2）如果点P在x轴上，且△ACD与△PBC相似，求点P的坐标；

（3）如果直线l与直线y=kx-6关于直线BC对称，求直线l的表达式．

 

 

Answer 1

（1）y=x2-2x-3；（2）y=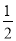x-．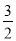

【解析】

试题分析：（1）将A坐标代入一次函数解析式求出k的值，进而求出B坐标，根据A为抛物线的顶点，设出抛物线顶点形式，将B坐标代入求出a的值，确定出抛物线解析式；

（2）由k的值确定出一次函数解析式，求出D的坐标，由抛物线解析式求出C坐标，由A的坐标得到∠DCA=45°，且AC=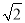，CD=3，根据B与C坐标得到∠OCB=45°，可得出∠DCA=∠OCB，由△ACD与△PBC相似，且点P在x轴上，得到点P在B点的左侧，分两种情况考虑：当△BPC∽△ACD时；当△BCP∽△CAD时，分别求出BP的长，即可确定出P的坐标；

（3）过点D作DH⊥BC并延长DH到点M，使HM=HD，连接CM、BM，可得直线BM即为直线l，且CM=CD，∠MCH=∠DCH，根据C与D坐标得到CM=CD，根据B与C坐标得到三角形BOC为等腰直角三角形，利用等腰三角形的性质得到∠OCB=45°，进而得到∠MCH=45°，∠MCD=90°，得出MC⊥y轴，确定出M坐标，设直线l的解析式为y=kx+b，将B与M坐标代入求出k与b的值，即可确定出直线l解析式．

试题解析：（1）∵y=kx-6过点A（1，-4），

∴-4=k-6，

∴k=2，即y=2x-6，

令y=0，得到x=3，即B（3，0），

∵以点A为顶点的抛物线经过点B，

∴设解析式为y=a（x-1）2-4，

将x=3，y=0代入得：0=a（3-1）2-4，

解得：a=1，

∴抛物线的表达式为y=x2-2x-3；

（2）∵k=2，

∴y=kx-6，即y=2x-6，

∴D（0，-6），

∵抛物线与y轴交于点C，

∴C（0，-3），

∵A（1，-4），

∴∠DCA=45°，且AC=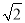，CD=3，

∵B（3，0），C（0，-3），

∴∠OCB=45°，

∴∠DCA=∠OCB，

∵△ACD与△PBC相似，且点P在x轴上，

∴点P在B点的左侧，

当△BPC∽△ACD时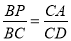，，即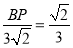，解得：BP=2；

当△BCP∽△CAD时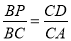，，即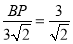，解得：BP=9，

∴BP=2或9，

∴点P坐标为（1，0）或（-6，0）；

（3）过点D作DH⊥BC并延长DH到点M，使HM=HD，连接CM、BM，

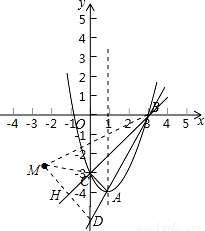
∴直线BM即为直线l，且CM=CD，∠MCH=∠DCH，

∵C（0，-3），D（0，-6），

∴CM=CD=3，

∵B（3，0），C（0，-3），

∴∠OCB=45°，

∴∠DCH=∠OCB=45°，

∴∠MCH=45°，

∴∠MCD=90°，即MC⊥y轴，

∵MC=CD=3，

∴M（-3，-3），

设直线l的解析式为y=kx+b，则，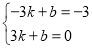

解得：，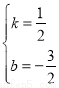

∴直线l的解析式为y=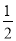x-．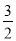

考点：二次函数综合题．