题目内容
如图,已知在△ABC中,∠C = 90°,AD = AC,DE⊥AB交BC于点E,若∠B = 28°,则∠AEC =
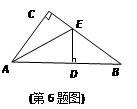
- A.28°
- B.59°
- C.60°
- D.62°
B
根据∠C=90°AD=AC,求证△CAE≌△DAE,∠CAE=∠DAE= ∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
解:∵在△ABC中,∠C=90°,
AD=AC,DE⊥AB交BC于点E,
∴△CAE≌△DAE,∴∠CAE=∠DAE= ∠CAB,
∠CAB,
∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°-28°=62°,
∵∠AEC=90°- ∠CAB=90°-31°=59°.
∠CAB=90°-31°=59°.
故选B.
此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证△CAE≌△DAE,此题稍微有点难度,属于中档题
根据∠C=90°AD=AC,求证△CAE≌△DAE,∠CAE=∠DAE=
 ∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.
∠CAB,再由∠C=90°,∠B=28°,求出∠CAB的度数,然后即可求出∠AEC的度数.解:∵在△ABC中,∠C=90°,
AD=AC,DE⊥AB交BC于点E,
∴△CAE≌△DAE,∴∠CAE=∠DAE=
 ∠CAB,
∠CAB,∵∠B+∠CAB=90°,∠B=28°,
∴∠CAB=90°-28°=62°,
∵∠AEC=90°-
 ∠CAB=90°-31°=59°.
∠CAB=90°-31°=59°.故选B.
此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证△CAE≌△DAE,此题稍微有点难度,属于中档题

练习册系列答案
相关题目

 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN. 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.