题目内容
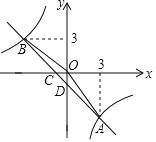
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A(2,2),B(n,4)两点,连接OA、OB.
的图象相交于A(2,2),B(n,4)两点,连接OA、OB.
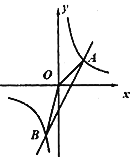
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)在直角坐标系中,是否存在一点P,使以P、A、O、B为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ;(2)
;(2)![]() 的面积为
的面积为![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为(-3,-6),(1,-2)(3,6).
的坐标为(-3,-6),(1,-2)(3,6).
【解析】
(1)根据反比例函数图象上点的坐标特征可求出k2和n的值,可得反比例函数解析式,再利用待定系数法即可求出一次函数的解析式;
(2)设一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 、
、![]() 分别向
分别向![]() 轴作垂线,垂足为点
轴作垂线,垂足为点![]() 、
、![]() ,令x=0,可求出点C的坐标,根据
,令x=0,可求出点C的坐标,根据![]() 即可得答案;
即可得答案;
(3)分OA、OB、AB为对角线三种情况,根据A、B坐标可得直线OA、OB的解析式,根据互相平行的两条直线斜率相同可知直线OP、AP、BP的斜率,利用待定系数法可求出其解析式,进而联立解析式求出交点坐标即可得答案.
(1)∵点![]() ,
,![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() ,
,![]() 在一次函数
在一次函数![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() .
.
(2)如图,设一次函数![]() 与y轴交于点
与y轴交于点![]() ,过点
,过点![]() 、
、![]() 分别向
分别向![]() 轴作垂线,垂足为点
轴作垂线,垂足为点![]() 、
、![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() 的面积为
的面积为![]() .
.

(3)∵点A(2,2),B(-1,-4),
∴直线OA的解析式为y=x,直线OB的解析式为y=4x,直线AB的解析式为y=2x-2,
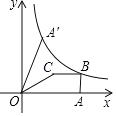
①如图,当OA//PB,OP//AB时,
∴直线OP的解析式为y=2x+b1,
设直线PB的解析式为y=x+b1,
∵点B(-1,-4)在直线上,
∴-4=-1+b1,
解得:b1=-3,
∴直线PB的解析式为y=x-3,
联立直线OP、BP解析式得:![]() ,
,
解得:![]() ,
,
∴点P坐标为(-3,-6),
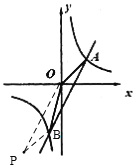
②如图,当OB//AP,OA//BP时,同①可得BP解析式为y=x-3,
设AP的解析式为y=4x+b2,
∵点A(2,2)在直线AP上,
∴2=2×4+b2,
解得:b2=-6,
∴直线AP的解析式为y=4x-6,
联立PB和AP解析式得:![]() ,
,
解得:![]() ,
,
∴点P坐标为(1,-2),
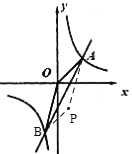
③如图,当OP//AB,OB//AP时,
同①②可得:直线OP的解析式为y=2x,直线AP的解析式为y=4x-6,
联立直线OP和AP解析式得:![]() ,
,
解得:![]() ,
,
∴点P坐标为(3,6),
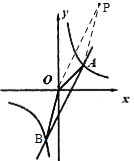
综上所述:存在点P,使以P、A、O、B为顶点的四边形是平行四边形,点![]() 的坐标为(-3,-6),(1,-2)(3,6).
的坐标为(-3,-6),(1,-2)(3,6).

 名校课堂系列答案
名校课堂系列答案【题目】商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了![]() 元.
元.
(1)填表:
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到最大时,则每台冰箱的实际售价应定为多少元?