题目内容
已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交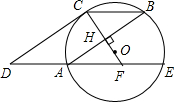 EA延长线于点D,延长CO交AE于点F.
EA延长线于点D,延长CO交AE于点F.(1)求证:CD为⊙O的切线;
(2)若BC=5,AB=8,求OF的长.
分析:(1)根据平行线的性质和垂直的定义推出∠DCF=90°,根据切线的判定即可判断;
(2)根据垂径定理得到AH=BH=3,根据勾股定理求出CH,证△HAF≌△HBC,得出FH=CH=3,CF=6,连接BO,设BO=x,则OC=x,
OH=x-3,由勾股定理得到42+(x-3)2=x2,求出方程的解,就能求出答案.
(2)根据垂径定理得到AH=BH=3,根据勾股定理求出CH,证△HAF≌△HBC,得出FH=CH=3,CF=6,连接BO,设BO=x,则OC=x,
OH=x-3,由勾股定理得到42+(x-3)2=x2,求出方程的解,就能求出答案.
解答:(1)证明:∵OC⊥AB,CD∥BA,
∴∠DCF=∠AHF=90°,
∴CD为⊙O的切线.
(2)解:∵OC⊥AB,AB=8,
∴AH=BH=
=4,
在Rt△BCH中,∵BH=4,BC=5,
由勾股定理得:CH=3,
∵AE∥BC,
∴∠B=∠HAF,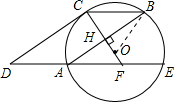
∵∠BHC=∠AHF,BH=AH,
∴△HAF≌△HBC,
∴FH=CH=3,CF=6,
连接BO,设BO=x,则OC=x,OH=x-3.
在Rt△BHO中,由勾股定理得:42+(x-3)2=x2,
解得x=
,
∴OF=CF-OC=
,
答:OF的长是
.
∴∠DCF=∠AHF=90°,
∴CD为⊙O的切线.
(2)解:∵OC⊥AB,AB=8,
∴AH=BH=
| AB |
| 2 |
在Rt△BCH中,∵BH=4,BC=5,
由勾股定理得:CH=3,
∵AE∥BC,
∴∠B=∠HAF,

∵∠BHC=∠AHF,BH=AH,
∴△HAF≌△HBC,
∴FH=CH=3,CF=6,
连接BO,设BO=x,则OC=x,OH=x-3.
在Rt△BHO中,由勾股定理得:42+(x-3)2=x2,
解得x=
| 25 |
| 6 |
∴OF=CF-OC=
| 11 |
| 6 |
答:OF的长是
| 11 |
| 6 |
点评:本题主要考查对全等三角形的性质和判定,垂径定理,勾股定理,平行线的性质,切线的判定,解一元一次方程等知识点的理解和掌握,能灵活运用这些性质进行证明是解此题的关键,题型较好,难度适中.

练习册系列答案
相关题目

 已知,如图直线l的解析式为y=x+4,交x、y轴分别于A、B两点,点M(-1,3)在直线l上,O为原点.
已知,如图直线l的解析式为y=x+4,交x、y轴分别于A、B两点,点M(-1,3)在直线l上,O为原点. 已知,如图直线l的解析式为y=x+4,交x、y轴分别于A、B两点,点M(-1,3)在直线l上,O为原点.
已知,如图直线l的解析式为y=x+4,交x、y轴分别于A、B两点,点M(-1,3)在直线l上,O为原点.
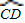 =
=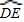 =
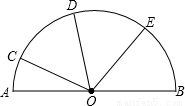
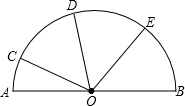
=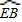 ,∠BOE=55°,则∠AOC的度数为 度.
,∠BOE=55°,则∠AOC的度数为 度.