题目内容
20、已知四边形ABCD的对角线AC、BD相交于点O,给出下列条件:①AB∥CD,②OA=OC,③AB=CD,④∠BAD=∠DCB,⑤AD∥BC.
(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示)
(2)从(1)中选出推理在两步以上的一种情况进行证明.(要求画出图形,写出证明过程即可)
(1)从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示)
①③,①⑤,①④,①②,②⑤,④⑤
;(至少写出三种情况)(2)从(1)中选出推理在两步以上的一种情况进行证明.(要求画出图形,写出证明过程即可)
分析:(1)根据平行四边形的5种判定方法,能推出四边形ABCD是平行四边形的有①③,①⑤,①④,①②,②⑤,④⑤;
(2)可选①②或①④,加以证明即可.
(2)可选①②或①④,加以证明即可.
解答:解:(1)①③,①⑤,①④,①②,②⑤,④⑤(写出三种情况即可)
(2)解法一:若选①②
如图

∵AB∥CD,
∴∠ABD=∠BDC.
又∵OA=OC,∠AOB=∠COD,
∴△ABO≌△CDO.
∴BO=DO.
∴四边形ABCD是平行四边形.
解法二:若选①④
如图

∵AB∥CD,
∴∠ABD+∠BCD=180度.
又∵∠BAD=∠DCB,
∴∠ABC+∠BAD=180度.
∴AD∥BC.
∴四边形ABCD是平行四边形.
(2)解法一:若选①②
如图

∵AB∥CD,
∴∠ABD=∠BDC.
又∵OA=OC,∠AOB=∠COD,
∴△ABO≌△CDO.
∴BO=DO.
∴四边形ABCD是平行四边形.
解法二:若选①④
如图

∵AB∥CD,
∴∠ABD+∠BCD=180度.
又∵∠BAD=∠DCB,
∴∠ABC+∠BAD=180度.
∴AD∥BC.
∴四边形ABCD是平行四边形.
点评:解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
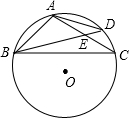 如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=
如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=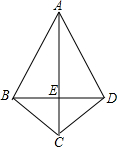 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为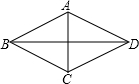 如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( )
如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( )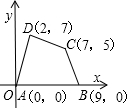 如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )
如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )