��Ŀ����
����Ŀ����֪����x����y��|��x2+bx��7|��4���㣨4��5���ں����ϣ���bΪ�����������������е��о������ľ��飬��Ըú�������ͼ���������̽����������������⣺
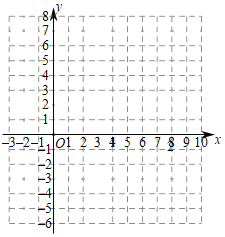
��1����b���� ����
��2������ͼ��̽����
���±���y��x�ļ����Ӧֵ����ֱ��д��m��n��ֵ��m���� ����n���� ����
x | �� | �� | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | �� |
y | �� | m | 3 |
| ��4 | 1 | 4 | n | 4 | 1 | ��4 |
| 3 | 5 | �� |
�ڸ�����ϲ���ķ�ʽ������ͼ��ʾ��ƽ��ֱ������ϵ�У������ú���ͼ��
��3���������ͼ��д���ú�����һ�����ʣ��� ����
��4��������x�ķ���|��x2+bx��7|��m+4���ĸ�������m��ȡֵ��ΧΪ�� ����
���𰸡���1��8����2����![]() ��5���ڼ���������3����������x��4�Գƣ���4����4��m��5.
��5���ڼ���������3����������x��4�Գƣ���4����4��m��5.
��������
��1�����㣨4��5�����뺯��y��|��x2+bx��7|��4�����b������������������⣻
��2������y��|��x2+8x��7|��4����x����![]() ʱ��y��
ʱ��y��![]() ����x��4ʱ��y��5������m��
����x��4ʱ��y��5������m��![]() ��n��5������㷨��ͼ���ɣ�
��n��5������㷨��ͼ���ɣ�
��3����������x��4�Գƣ���д��һ�����ɣ�
��4�����ͼ���ң���x��4ʱ��y��5����x��1��x��7ʱ��y����4����4��m��5ʱ��|��x2+8x��7|��m+4���ĸ�����
�⣺��1�����㣨4��5�����뺯��y��|��x2+bx��7|��4��
��b��8��b��3��5��
��b������
��b��8��
�ʴ�Ϊ8��
��2���١�b��8��
��y��|��x2+8x��7|��4��
��x����![]() ʱ��y��
ʱ��y��![]() ��
��
��x��4ʱ��y��5��
��m��![]() ��n��5��
��n��5��
�ʴ�Ϊ![]() ��5��
��5��
����ͼ��ʾ��
��3����������x��4�Գƣ�
��4����x��4ʱ��y��5��
��x��1��x��7ʱ��y����4��
�൱��4��m��5ʱ��|��x2+8x��7|��m+4���ĸ�����
�ʴ�Ϊ��4��m��5��


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�