题目内容
【题目】已知等腰△ABC中，AD垂直于直线BC，垂足为点D，且AD＝
BC，则△ABC底角的度数为( )
A. 45° B. 75° C. 45°或75°或15° D. 60°
【答案】C
【解析】
分三种情况讨论，先根据题意分别画出图形，当AB=AC时，根据已知条件得出AD=BD=CD，从而得出△ABC底角的度数；当AB=BC时，先求出∠ABD的度数，再根据AB=BC，求出底角的度数；当AB=BC时，根据AD=
BC，AB=BC，得出∠DBA=30°，从而得出底角的度数．
①如图1，当AB=AC时，
∵AD⊥BC，∴BD=CD，
∵AD=BC，∴AD=BD=CD，∴底角为45°；
②如图2，当AB=BC时，
∵AD=BC，∴AD=AB，∴∠ABD=30°，∴∠BAC=∠BCA=75°，∴底角为75°．
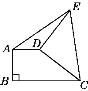
③如图3，当AB=BC时，
∵AD=BC，AB=BC，∴AD=AB，∴∠DBA=30°，∴∠BAC=∠BCA=15°；
∴△ABC底角的度数为45°或75°或15°．
故选C．
练习册系列答案
相关题目
