题目内容
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1 , 将Cl绕点B中心对称变换得C2 , C2与x轴交于另一点C,将C2绕点C中心对称变换得C3 , 连接C,与C3的顶点,则图中阴影部分的面积为( ) 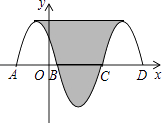
A.32
B.24
C.36
D.48
【答案】A
【解析】解:∵y=﹣x2﹣2x+3=﹣(x+1)2+4, ∴C1的顶点坐标为(﹣1,4).
当y=0时,有﹣x2﹣2x+3=0,
解得:x1=﹣3,x2=1,
∴点A的坐标为(﹣3,0),点B的坐标为(1,0).
∵将Cl绕点B中心对称变换得C2 , 将C2绕点C中心对称变换得C3 ,
∴C2的顶点坐标为(3,﹣4),点C的坐标为(5,0),C3的顶点坐标为(7,4),
∴S阴影=[7﹣(﹣1)]×(4﹣0)=8×4=32.
故选A.
【考点精析】解答此题的关键在于理解二次函数图象的平移的相关知识,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目