题目内容
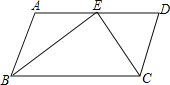
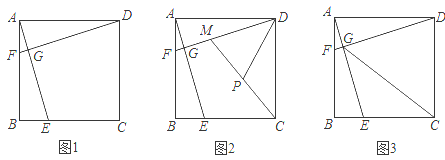
【题目】如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.
(1)求证:AE=DF.
(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.
(3)如图3,连接CG.若CG=BC,则AF:FB的值为 .
【答案】(1)见解析;(2)DG=![]() DP,理由见解析;(3)1∶1.
DP,理由见解析;(3)1∶1.
【解析】
(1)用SAS证△ABE≌△DAF即可;
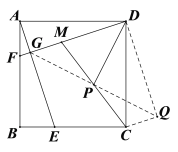
(2)DG=![]() DP,连接GP并延长至点Q,使PQ=PG,连接CQ,DQ,先用SAS证△PMG≌△PCQ,得CQ=MG=AG,进一步证明∠DAG=∠DCQ,再用SAS证明△DAG≌△DCQ,得∠ADF=∠CDQ,于是有∠FDQ=90°,进而可得△DPG为等腰直角三角形,由此即得结论;
DP,连接GP并延长至点Q,使PQ=PG,连接CQ,DQ,先用SAS证△PMG≌△PCQ,得CQ=MG=AG,进一步证明∠DAG=∠DCQ,再用SAS证明△DAG≌△DCQ,得∠ADF=∠CDQ,于是有∠FDQ=90°,进而可得△DPG为等腰直角三角形,由此即得结论;
(3)延长AE、DC交于点H,由条件CG=BC可证CD=CG=CH,进一步用SAS证△ABE≌△HCE,得BE=CE,因为AF=BE,所以AF:BF=BE:CE=1:1.
解:(1)证明:正方形ABCD中,
AB=AD,∠ABE=∠DAF=90°,BE=AF,
∴△ABE≌△DAF(SAS)
∴AE=DF;
(2)DG=![]() DP,理由如下:
DP,理由如下:
如图,连接GP并延长至点Q,使PQ=PG,连接CQ,DQ,
∵PM=PC,∠MPG=∠CPQ,
∴△PMG≌△PCQ(SAS),
∴CQ=MG=AG,∠PGM=∠PQC,
∴CQ∥DF,
∴∠DCQ=∠FDC=∠AFG,
∵∠AFG+∠BAE=90°,∠DAG+∠BAE=90°,
∴∠AFG=∠DAG.
∴∠DAG=∠DCQ.
又∵DA=DC,
∴△DAG≌△DCQ(SAS).
∴∠ADF=∠CDQ.
∵∠ADC=90°,
∴∠FDQ=90°.
∴△GDQ为等腰直角三角形
∵P为GQ的中点
∴△DPG为等腰直角三角形.
∴DG=![]() DP.
DP.
(3)1∶1.
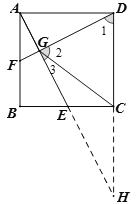
证明:延长AE、DC交于点H,
∵CG=BC,BC=CD,
∴CG=CD,∴∠1=∠2.
∵∠1+∠H=90°,∠2+∠3=90°,
∴∠3=∠H.
∴CG=CH.
∴CD=CG=CH.
∵AB=CD,∴AB=CH.
∵∠BAE=∠H,∠AEB=∠HEC,
∴△ABE≌△HCE(SAS).
∴BE=CE.
∵AF=BE,
∴AF:BF=BE:CE=1:1.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
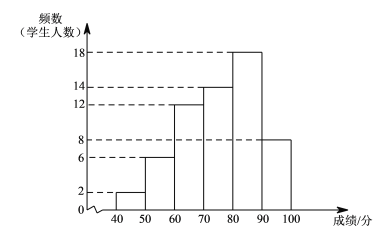
冲刺100分单元优化练考卷系列答案【题目】某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .A课程成绩的频数分布直方图如下(数据分成6组:
.A课程成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
![]() .A课程成绩在
.A课程成绩在![]() 这一组是:
这一组是:
70 71 71 71 76 76 77 78 ![]()
![]() 79 79 79
79 79 79 ![]()
![]() .A,B两门课程成绩的平均数、中位数、众数如下:
.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过![]() 分的人数.
分的人数.
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
级别 | 家庭的文化教育消费金额 | 户数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
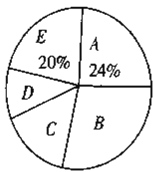
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有___________户,表中![]() ___________;
___________;
(2)在扇形统计图中,![]() 组所在扇形的圆心角为多少度?
组所在扇形的圆心角为多少度?
(3)这个社区有![]() 户家庭,请你估计年文化教育消费在
户家庭,请你估计年文化教育消费在![]() 元以上的家庭有多少户.
元以上的家庭有多少户.