题目内容
如图,已知二次函数y=ax2-4x+c的图像经过点A和点B.(1)求该二次函数的表达式;
(2)点E(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求Q到y轴的距离.
(3)设抛物线与y轴的的交点为C,点P为抛物线的对称轴上的一动点,求使∠PCB=90°的点P的坐标.
(1)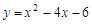 ,(2)2,(3)(2,-4)解析:
,(2)2,(3)(2,-4)解析:
解:(1)将x=-1,y=-1;x=3,y=-9分别代入 得
得
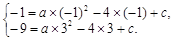 解得
解得 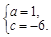
∴二次函数的表达式为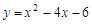 .……………………4分
.……………………4分
(2)将(m,m)代入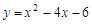 ,得
,得 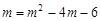 ,
,
解得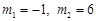 .∵m>0,∴
.∵m>0,∴ 不合题意,舍去.
不合题意,舍去.
∴ m=6.…………………………………………6分
∵点E与点Q关于对称轴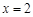 对称,∴点Q的的坐标是(-2,6),
对称,∴点Q的的坐标是(-2,6),
∴点Q到y轴的距离为2………………………8分
(3)∵B点坐标为(-9,3),点C的的坐标为(0,-6)则∠BCN= 45°, ……………10分
∵∠PCB=90°,∴ ∠PCN= 45°, ∴PN="NC=2," ∴P点坐标为(2,-4)………………12分
(1)通过A、B两点的坐标求出二次函数的表达式,(2)将(m,m)代入二次函数,求得m的值,点E与点Q关于对称轴对称,求出点Q的的坐标,从而求得点Q到y轴的距离,(3)通过C、B两点的坐标求出∠BCN= 45°,要使∠PCB=90°,就得 ∠PCN= 45°,即PN=NC=2,从而求得点P的坐标
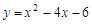 ,(2)2,(3)(2,-4)解析:
,(2)2,(3)(2,-4)解析:解:(1)将x=-1,y=-1;x=3,y=-9分别代入
 得
得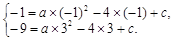 解得
解得 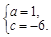
∴二次函数的表达式为
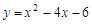 .……………………4分
.……………………4分(2)将(m,m)代入
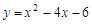 ,得
,得 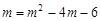 ,
,解得
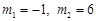 .∵m>0,∴
.∵m>0,∴ 不合题意,舍去.
不合题意,舍去.∴ m=6.…………………………………………6分
∵点E与点Q关于对称轴
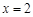 对称,∴点Q的的坐标是(-2,6),
对称,∴点Q的的坐标是(-2,6),∴点Q到y轴的距离为2………………………8分
(3)∵B点坐标为(-9,3),点C的的坐标为(0,-6)则∠BCN= 45°, ……………10分
∵∠PCB=90°,∴ ∠PCN= 45°, ∴PN="NC=2," ∴P点坐标为(2,-4)………………12分
(1)通过A、B两点的坐标求出二次函数的表达式,(2)将(m,m)代入二次函数,求得m的值,点E与点Q关于对称轴对称,求出点Q的的坐标,从而求得点Q到y轴的距离,(3)通过C、B两点的坐标求出∠BCN= 45°,要使∠PCB=90°,就得 ∠PCN= 45°,即PN=NC=2,从而求得点P的坐标

练习册系列答案
相关题目
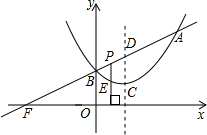 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.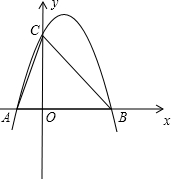
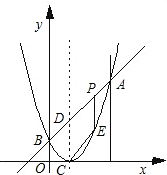 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.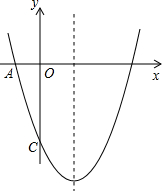 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5). (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数