题目内容
【题目】解方程（组）、不等式（组）：
（1）
．
（2）
．
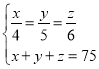（3）
．
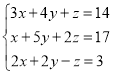（4）
．
（5）解不等式组：
并把解集在数轴上表示出来．
【答案】（1）
；（2）
；（3）
；（4）
；（5）
，数轴见解析
【解析】
（1）先去分母，化为：
，然后依次去括号，移项，合并同类项，系数化为1进行求解；
（2）设
，那么
，将
代入第二个方程解出
，那么就可以求得；
（3）用①+③消掉
得到④，然后用①×2-②得到⑤，联立④和⑤解出
再代入③求出；
（4）先去分母，化为：
，然后依次去括号，移项，合并同类项，系数化为1进行求解；
（5）分别求出两个不等式的解集，然后按照解集的判断方法求解即可；
（1）原方程可化为：
原方程的解为：
（2）设
将其代入
可得：
解得：
原方程组的解为：
（3）
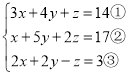
①+③可得：
④
①×2-②可得：
⑤
④-⑤可得：
将代入④解得：
将，代入③可得：
原方程组的解为：
（4）原不等式可化为：
原不等式的解集为：
（5）
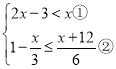
解不等式①可得：
解不等式②可得：
原不等式组的解集为：
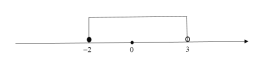
画出数轴如下所示：
练习册系列答案
相关题目
【题目】已知二次函数y=x2﹣2x﹣1．
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
（1）请在表内的空格中填入适当的数；
（2）根据列表，请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象；
（3）当x在什么范围内时，y随x增大而减小；
