题目内容
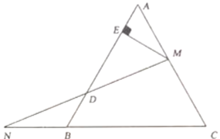
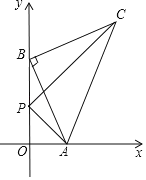
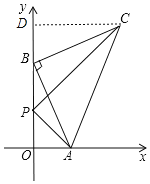
【题目】如图,在平面直角坐标系中,等腰直角△ABC,AB⊥BC,AB=BC,点C在第一象限.已知点A(m,0),B(0,n)(n>m>0),点P在线段OB上,且OP=OA.
(1)点C的坐标为 (用含m,n的式子表示)
(2)求证:CP⊥AP.
【答案】(1)(n,m+n);(2)详见解析.
【解析】
(1)过点C作CD⊥y轴于点D,由“AAS”可证△CDB≌△BOA,可得BO=CD=n,AO=BD=m,即可求解;
(2)由线段的和差关系可得DP=n=DC,可得∠DPC=45°,可得结论.
(1)如图,过点C作CD⊥y轴于点D,
∴∠CDB=90°,
∴∠DCB+∠DBC=90°,且∠ABO+∠CBD=90°,
∴∠DCB=∠ABO,且AB=BC,∠CDB=∠AOB=90°,
∴△CDB≌△BOA(AAS)
∴BO=CD=n,AO=BD=m,
∴OD=m+n,
∴点C(n,m+n),
故答案为:(n,m+n);
(2)∵OP=OA=m,OD=m+n,
∴DP=n=DC,∠OPA=45°,
∴∠DPC=45°,
∴∠APC=90°,
∴AP⊥PC.

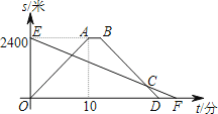
【题目】如图,△ABC中,AB=BC=5cm,AC=6cm,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,BP长度为ycm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:
(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.5 | 4.1 | 4 | 4.5 | 5.0 |
要求:补全表格中相关数值(保留一位小数);
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
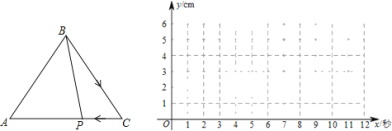
(3)结合画出的函数图象,解决问题:当x约为______时,BP=CP.
【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.