题目内容
 如图,△ABC的面积为1,D、E分别在AB,AC上,且DE∥BC,P在BC延长线上一点,则△DEP面积的最大值是________.
如图,△ABC的面积为1,D、E分别在AB,AC上,且DE∥BC,P在BC延长线上一点,则△DEP面积的最大值是________.

分析:设BC=a,DE=b,BC上的高=h,DE与BC的距离=x,利用三角形的面积公式和相似三角形的性质:对应高之比等于相似比,和得到△DEP面积和DE之间的二次函数关系,利用二次函数的性质求其最值即可.
解答:设BC=a,DE=b,BC上的高=h,DE与BC的距离=x,
∵△ABC的面积为1,即
 ah=1,
ah=1,
∴ah=2,
∵DE∥BC,
∴△ADE∽△ABC,
∴
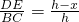 ,
,即

∴x=
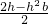 ,
,∴S△DEP=
 b×x=
b×x= b
b =-
=- h2b2+
h2b2+ bh,
bh,∵△ABC的高h是一定值,
∴S△DEP是边DE的二次函数,
∵二次项系数为-
 ,
,∴函数有最大值为:s=
 =
= ,
,故答案为:

点评:本题考查了三角形的面积最值的问题,解题的关键是建立面积和边(或高)的二次函数关系,利用二次函数的性质求其最值即可.

练习册系列答案
相关题目
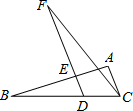 如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是
如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是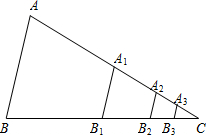 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为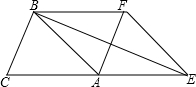 如图,△ABC的面积为
如图,△ABC的面积为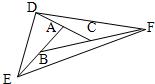 3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF=
3、如图,△ABC的面积为1,若把△ABC的各边分别延长一倍,得到一个新的△DEF,则S△DEF=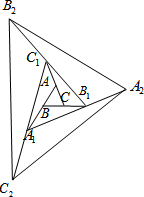 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过