题目内容
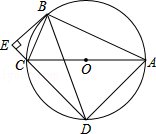
【题目】如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=( ) 
A.2:5:25
B.4:9:25
C.2:3:5
D.4:10:25
【答案】D
【解析】解:根据图形知:△DEF的边DF和△BFE的边BF上的高相等,并设这个高为h, ∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∵DE:EC=2:3,
∴DE:AB=2:5,
∵DC∥AB,
∴△DEF∽△BAF,
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= 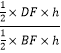 =
= ![]() =
= ![]() =
= ![]()
∴S△DEF:S△EBF:S△ABF=4:10:25,
故选D.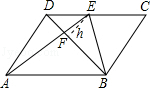
【考点精析】利用三角形的面积和平行四边形的性质对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

 名校课堂系列答案
名校课堂系列答案【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |