题目内容

已知△ABC的三个内角，∠A、∠B、∠C满足关系式∠B+∠C=
1
2
∠A，则此三角形（　　）
A、一定是直角三角形
B、-定有一个内角为45°
C、一定是钝角三角形
D、一定是锐角三角形
分析：利用三角形内角和定理，可得∠A+∠B+∠C=180°①，把已知∠B+∠C=
1
2
∠A整体代入①，可得关于∠A的一元一次方程，求解即可．
解答：解：∵∠A+∠B+∠C=180°，∠B+∠C=
1
2
∠A，
∴∠A+
1
2
∠A=180°，
∴∠A=120°，
∴△ABC是钝角三角形．
故选C．
点评：本题利用了三角形内角和定理、整体代入、解一元一次方程的知识．
练习册系列答案
相关题目
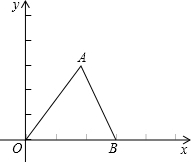精英家教网如图，在平面直角坐标系中，已知：△ABC的三个顶点的坐标分别是A（4，6）、B（0，0）、C（6，0）．
（1）求AO、AB所在直线的函数解析式；
（2）在△AOB内可以作一个正方形CDEF，使它的三个顶点分别落在边AO、AB上，E、F两个顶点落在OB上，请求出这个正方形四个顶眯的坐标，并在图中画出这个正方形；
（3）连接OC，在线段OC上任取一点P，过P作与x轴、y轴的不行线与OA、OB分别交于M、N两点，过M作OB边的垂线与OB交于H；你有什么发现？请写出来，并说明理由．
附加题：
（1）如图，AB、CD是⊙O的两条弦，它们相交于点P，连接AD、BD，已知AD=BD=4，PC=6，那么CD的长是
 
．
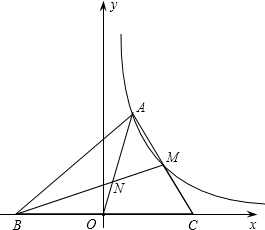精英家教网
（2）阅读材料：如图，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=
1
2
ah，即三角形面积等于水平宽与铅垂高乘积的一半．
精英家教网
解答下列问题：
如图，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．
①求抛物线和直线AB的解析式；
②点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；
③点P是抛物线（在第一象限内）上的一个动点，是否存在一点P，使S△PAB=
9
8
S△CAB，若存在，求出P点的坐标；若不存在，请说明理由．
精英家教网
23、已知△ABC在坐标平面内三顶点的坐标分别为A（0，2）、B（3，3）、C（2，1）．以B为位似中心，画出△Α1Β1С1与△ABC相似（与图形同向），且相似比是2的三角形，它的三个对应顶点的坐标分别是：
Α1（
-3
，
1
）；B1（
3
，
3
）；С1（
1
，
-1
）
如图1，抛物线y=ax2-5ax+4经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．
（1）求抛物线的解析式；

（2）若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形，若存在，求出所有符合条件的点P坐标；不存在，请说明理由；
（3）如图2，将△AOC沿x轴对折得到△AOC1，再将△AOC1绕平面内某点旋转180°后得△A1O1C2（A，O，C1分别与点A1，O1，C2对应）使点A1，C2在抛物线上，求A1，C2的坐标．
已知，如图：在平面直角坐标系中，O是坐标原点，△ABC的三个顶点坐精英家教网标分别是A（1，2
3
），B（-3，0），C（3，0），直线AC与反比例函数y=
k
x
在第一象限内的图象相交于A，M两点．
（1）求反比例函数y=
k
x
的解析式；
（2）连接BM交AO于点N，求证：N是△ABC的重心；
（3）在直线AC上是否存在一点P使△BPO的周长L取得最小值？若存在，求出L的最小值并证明；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网