题目内容
已知,如图:在平面直角坐标系中,O是坐标原点,△ABC的三个顶点坐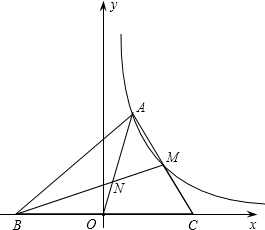 标分别是A(1,2
标分别是A(1,2| 3 |
| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)连接BM交AO于点N,求证:N是△ABC的重心;
(3)在直线AC上是否存在一点P使△BPO的周长L取得最小值?若存在,求出L的最小值并证明;若不存在,请说明理由.
分析:本题是一次函数和反比例函数以及三角形的重心、轴对称相结合的一道综合试题.要求反比例函数的解析式,而点A图象上,将其坐标代入即可;要求点N是三角形的重心.由已知B、C的坐标可知O是BC的中点.只要求出M是AC的中点就可,可以求出AC的解析式,利用反比例函数和一次函数的解析式求出M点的坐标,过点A、M作x轴的垂线于D、C.求出D、C的坐标从而求出DC、EC的长,由相似得到M是AC的中点,得N是重心;利用轴对称找到O点关于AC的对称点O|,作其x轴的垂线,连接CO|,由三角函数求出∠ACD、∠ACO|,的度数,求出O|,的长度在加上BO的长度就是L的最小值.
解答:解:(满分12分)(1)点A在y=
的图象上,∴2
=
k=2
(2分)
∴y=
(2)设经过A、C的直线的表达式为y=k1x+b由A(1,2
),C(3,0),
k 1=-
,b=3
(4分)(各1分)
∴经过AC的直线的表达式为y=-
x+3
∵直线AC与y=
的图象交点为M,且k=2
,
∴直线y=-
x+3
与双曲线y=
在M点的纵坐标相等,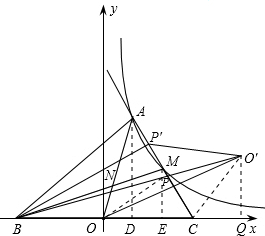
∴
=-
x+3
,(5分)
解得:x=1或x=2,经检验都是原方程的根
∴A(1,2
)和M(2,
)(6分)
过A作垂线段AD⊥BC,垂足为D,则D(1,0)∴DC=2
过M作垂线段ME⊥BC,垂足为E,则E(2,0)∴EC=1
易证△CME∽△CAD,∴
=
=
,∴CM=
CA,M是AC中点,BM是△ABC的中线
又B(-3,0),C(3,0),∴O是BC中点,AO是△ABC的中线,∴N是△ABC的重心(7分)
(3)过O作直线AC的对称点O′,连接BO′交AC于P,
连接BP,PO,则△BPO周长最小.(9分)
证明:∵O和O′关于直线AC对称,∴PO=PO′,∴BP+OP=BO′
在直线AC上任取异于P的点P′,连接BP′,OP′,P′O′,
则BP′+OP′=BP′+P′O′>BO′,(10分)
∴BO′是BP+OP的最小值.又BO是定值,
∴此时△BPO周长L最小.
O、O′关于直线AC对称,∴△CPO≌△CPO′
OC=CO′=3,又AD=2
,DC=2,
∴tan∠ACD=
=
=
,
∴∠ACD=60°,∴∠PCO'=∠ACD=60°,
∴CQ=1.5,QO′=
又BQ=BC+CQ=6+
=7
∴
∴最小值L=3
+3(12分)
| k |
| x |
| 3 |
| k |
| 1 |
| 3 |
∴y=
2
| ||
| x |
(2)设经过A、C的直线的表达式为y=k1x+b由A(1,2
| 3 |
|
| 3 |
| 3 |
∴经过AC的直线的表达式为y=-
| 3 |
| 3 |
∵直线AC与y=
| k |
| x |
| 3 |
∴直线y=-
| 3 |
| 3 |
2
| ||
| x |

∴
2
| ||
| x |
| 3 |
| 3 |
解得:x=1或x=2,经检验都是原方程的根
∴A(1,2
| 3 |
| 3 |
过A作垂线段AD⊥BC,垂足为D,则D(1,0)∴DC=2
过M作垂线段ME⊥BC,垂足为E,则E(2,0)∴EC=1
易证△CME∽△CAD,∴
| CE |
| CD |
| CM |
| CA |
| 1 |
| 2 |
| 1 |
| 2 |
又B(-3,0),C(3,0),∴O是BC中点,AO是△ABC的中线,∴N是△ABC的重心(7分)
(3)过O作直线AC的对称点O′,连接BO′交AC于P,
连接BP,PO,则△BPO周长最小.(9分)
证明:∵O和O′关于直线AC对称,∴PO=PO′,∴BP+OP=BO′
在直线AC上任取异于P的点P′,连接BP′,OP′,P′O′,
则BP′+OP′=BP′+P′O′>BO′,(10分)
∴BO′是BP+OP的最小值.又BO是定值,
∴此时△BPO周长L最小.
O、O′关于直线AC对称,∴△CPO≌△CPO′
OC=CO′=3,又AD=2
| 3 |
∴tan∠ACD=
| AD |
| DC |
2
| ||
| 2 |
| 3 |
∴∠ACD=60°,∴∠PCO'=∠ACD=60°,
∴CQ=1.5,QO′=
| 3 |
| 2 |
| 3 |
又BQ=BC+CQ=6+
| 3 |
| 2 |
| 1 |
| 2 |
∴
|
∴最小值L=3
| 7 |
点评:本题是一道综合性较强,难度较大的综合题目,解答中要注意运用数形结合的思想,利用解析式求交点坐标,运用轴对称知识,三角形的相似和全等以及解直角三角形的知识.解答中将图形和数值结合.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

