题目内容
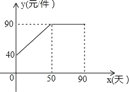
【题目】九年级(3)班数学兴趣小组经过市场调查整理发现某种商品的销售量P(件)与销售时间x天(1≤x≤90,且x为整数)成一次函数关系,具体数量关系如下表.已知商品的进价为30元/件,该商品的售价y(元/件)与销售时间x天的函数关系如图所示,每天的销售利润为w(元).

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
【答案】(1)w=![]() ;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
【解析】分析:(1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50≤x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,代入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当1≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50≤x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
详解:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b.
∵y=kx+b经过点(0,40)、(50,90),∴![]() ,解得:
,解得:![]() ,∴售价y与时间x的函数关系式为y=x+40;
,∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90,∴售价y与时间x的函数关系式为y=![]() .
.
由每天的销售量p与时间x成一次函数关系,设每天的销售量p与时间x的函数关系式为p=mx+n.
∵p=mx+n过点(60,80)、(30,140),∴![]() ,解得:
,解得:![]() ,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;
,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;
当50<x≤90时,w=(90﹣30)(﹣2x+200)=﹣120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是
w=![]() .
.
(2)当0≤x≤50时,w=﹣2x2+180x+2000=﹣2(x﹣45)2+6050.
∵a=﹣2<0且0≤x≤50,∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,
∵k=﹣120<0,w随x增大而减小,∴当x=50时,w取最大值,最大值为6000元.
∵6050>6000,∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当1≤x≤50时,令w=﹣2x2+180x+2000≥5600,即﹣2x2+180x﹣3600≥0,解得:30≤x≤50,50﹣30+1=21(天);
当50≤x≤90时,令w=﹣120x+12000≥5600,即﹣120x+6400≥0,解得:50≤x≤53![]() .
.
∵x为整数,∴50≤x≤53,53﹣50+1=4(天).
综上可知:21+4﹣1=24(天),故该商品在销售过程中,共有24天每天的销售利润不低于5600元.

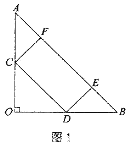
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

【题目】(本题有两道题,请从(1)、(2)题中选一题作答即可)
(1)某品牌太阳镜由一个镜架和两个镜片配套构成,每个工人每天可以加工![]() 个镜架或者加工
个镜架或者加工![]() 个镜片,现有
个镜片,现有![]() 名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
名工人,应怎么安排人力,才能使每天生产的镜架和镜片配套?能做成多少副太阳镜?
(2)去年春季,蔬菜种植场在![]() 公顷的大棚地里分别种植了茄子和西红柿,总费用是
公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
万元.其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 万元 | 每公顷获利 万元 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
①求出茄子和西红柿的种植面积各为多少公顷?
②种植场在这一季共获利多少万元?