题目内容
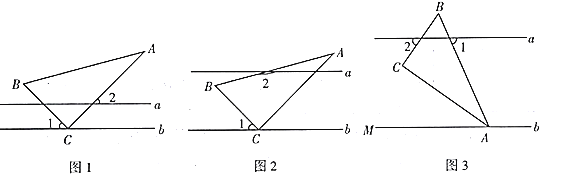
【题目】如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于（ ）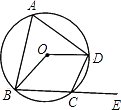
A.69°
B.42°
C.48°
D.38°
【答案】A
【解析】解：∵∠BOD=138°，
∴∠A= 
∠BOD=69°，
∴∠BCD=180°﹣∠A=111°，
∴∠DCE=180°﹣∠BCD=69°．
所以答案是：A．
【考点精析】解答此题的关键在于理解圆周角定理的相关知识，掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半，以及对圆内接四边形的性质的理解，了解把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x+40 | 90 |
每天销量（件） | 200﹣2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
