��Ŀ����
������̽����ͼ��
��֪��ABC��
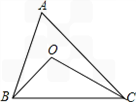
��1��������B����C��ƽ���ߣ����ڵ�O��
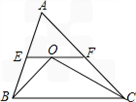
��2������O��EF��BC����AB�ڵ�E��AC�ڵ�F��
��3��д������ͼ����ĸ��ʾ����ȵĽǣ���˵�����ɣ�
��4������ABC=80�㣬��ACB=60�㣬���A����BOC�Ķ�����������ABC=70�㣬��ACB=50�㣬���A����BOC�Ķ�����
��5�����ݣ�4���Ľ������³���BOC���A�����Ĵ�С��ϵ������۶�����һ�������ζ�������Ϊʲô��
��֪��ABC��
��1��������B����C��ƽ���ߣ����ڵ�O��
��2������O��EF��BC����AB�ڵ�E��AC�ڵ�F��
��3��д������ͼ����ĸ��ʾ����ȵĽǣ���˵�����ɣ�
��4������ABC=80�㣬��ACB=60�㣬���A����BOC�Ķ�����������ABC=70�㣬��ACB=50�㣬���A����BOC�Ķ�����
��5�����ݣ�4���Ľ������³���BOC���A�����Ĵ�С��ϵ������۶�����һ�������ζ�������Ϊʲô��
�⣺����ͼ
 ��
��
����ͼ
�ۡ�AEF=��ABC����AFE=��ACB����ֱ��ƽ�У�ͬλ����ȣ�������EOB=��OBC=��EBO����FOC=��OCB=��FCO����ֱ��ƽ�У��ڴ�����ȣ���ƽ���ߵ����ʣ���
�ܵ���ABC=80�㣬��ACB=60��ʱ����A=180�㩁80�㩁60��=40�㣻��BOC=180�㩁 ����B+��C��=180�㩁
����B+��C��=180�㩁 �ϣ�180�㩁��A��=90��+
�ϣ�180�㩁��A��=90��+ ��A=110�㣻
��A=110�㣻
ͬ������ABC=70�㣬��ACB=50�㣬��A=60�㣬��BOC=120�㣻
�ݡ�BOC=90��+ ��A������
��A������
֤�����ߡ�BOC=��180�㩁��OBC����OCB��
�ߡ�OBC= ��B����OCB=
��B����OCB= ��C���ҡ�A+��B+��C=180�㣬
��C���ҡ�A+��B+��C=180�㣬
���BOC=180�㩁 ����B+��C��=180�㩁
����B+��C��=180�㩁 �ϣ�180�㩁��A��=90��+
�ϣ�180�㩁��A��=90��+ ��A��
��A��
 ��
������ͼ

�ۡ�AEF=��ABC����AFE=��ACB����ֱ��ƽ�У�ͬλ����ȣ�������EOB=��OBC=��EBO����FOC=��OCB=��FCO����ֱ��ƽ�У��ڴ�����ȣ���ƽ���ߵ����ʣ���
�ܵ���ABC=80�㣬��ACB=60��ʱ����A=180�㩁80�㩁60��=40�㣻��BOC=180�㩁
 ����B+��C��=180�㩁
����B+��C��=180�㩁 �ϣ�180�㩁��A��=90��+
�ϣ�180�㩁��A��=90��+ ��A=110�㣻
��A=110�㣻ͬ������ABC=70�㣬��ACB=50�㣬��A=60�㣬��BOC=120�㣻
�ݡ�BOC=90��+
 ��A������
��A������֤�����ߡ�BOC=��180�㩁��OBC����OCB��
�ߡ�OBC=
 ��B����OCB=
��B����OCB= ��C���ҡ�A+��B+��C=180�㣬
��C���ҡ�A+��B+��C=180�㣬���BOC=180�㩁
 ����B+��C��=180�㩁
����B+��C��=180�㩁 �ϣ�180�㩁��A��=90��+
�ϣ�180�㩁��A��=90��+ ��A��
��A��
��ϰ��ϵ�д�
 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
�����Ŀ
 ������̽��
������̽��
 ������̽��
������̽��