题目内容
【题目】如图，直线 
分别与x轴，y轴相交于A，B两点，0为坐标原点，A点的坐标为(4，0)
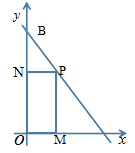
（1）求k的值；
（2）过线段AB上一点P(不与端点重合)作x轴，y轴的垂线，垂足分别为M，N。当长方形PMON的周长是10时，求点P的坐标。
【答案】
（1）解：∵直线y=kx+8经过A（4，0），
∴0=4k+8，
∴k=-2．
（2）∵四边形PNOM是矩形，
∵PN⊥y轴，PM⊥x轴，
∵点P在直线y=-2x+8上，PN=t，
∴P（t，-2t+8），
∴PM=-2t+8，
∴四边形PNOM的周长=[t+（-2t+8）]
=10，解得t=3
∴点P的坐标为（3，2）
【解析】（1）利用待定系数法，把A点坐标代入即可；（2）利用周长为10这个等量关系，用P的横坐标分别表示矩形的一组邻边，建立方程，求出坐标.
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】某班测量了10名学生的身高，他们的身高与对应的人数如下表所示
身高（cm） | 163 | 165 | 170 | 172 | 173 |
学生人数（人） | 1 | 2 | 3 | 2 | 2 |
则这10名学生身高的众数和中位数分别为（ ）
A.165cm，165cmB.170cm，165cm
C.165cm，170cmD.170cm，170cm
