题目内容
【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求: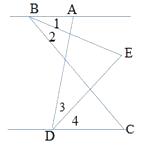
(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数。(用含n的式子表示)
【答案】
(1)∵AB//CD,
∴∠BAD=∠ADC
又∵∠BAD=80°,
∴∠ADC=80°.
∵BE平分∠ABC,
∴∠EDC=![]() ∠ADC=40°.
∠ADC=40°.
(2)过点E作EF//AB,则有∠BEF=∠1.
又∵AB//CD,EF//AB
∴EF//CD.
∴∠ABC=∠BCD=n°.
又∵BE平分∠ABC,
∴∠1=![]() ∠ABC=
∠ABC=![]() .
.
∠BEF=![]()
∴∠BED=∠BEF+∠FED=![]() .
.
【解析】(1)根据平行线的性质,两直线平行内错角相等得∠ADC=800,在根据平分线定义即可求得;
(2)平行线间出现折线时,可过折点作平行线,证出∠BED=∠ABE+∠EDC,进而表示出![]() BED的度数.
BED的度数.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目