题目内容
【题目】已知抛物线y=mx2+(2﹣2m)x+m﹣2(m是常数).
(1)无论m取何值,该抛物线都经过定点 D.直接写出点D的坐标.
(2)当m取不同的值时,该抛物线的顶点均在某个函数的图象上,求出这个函数的表达式.
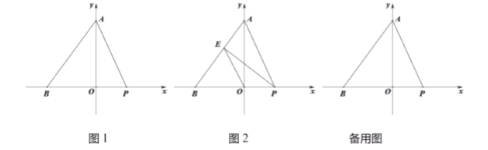
(3)若在0≤x≤1的范围内,至少存在一个x的值,使y>0,求m的取值范围.
【答案】(1) 定点D(1,0);(2)在;(3)m>2.
【解析】
①当x=1时,y=0.说明无论m取何值,函数图像都经过同一个点(1,0),可求定点.
②根据抛物线方程求出顶点坐标,进而求出函数表达式.
③根据一二问求出抛物线与x轴的交点,再讨论对称轴与交点坐标的位置关系.
解:(1)∵抛物线y=mx2+(2﹣2m)x+m﹣2=m(x﹣1)2+2(x﹣1)
∴当x﹣1=0时,无论m为何值,抛物线经过定点 D,
∴x=1,y=0,
∴定点D(1,0);
(2)∵﹣![]() =﹣
=﹣![]() =1﹣
=1﹣![]() ,
,
![]() =
=![]() =﹣
=﹣![]() ,
,
∴顶点为(1﹣![]() ,﹣
,﹣![]() ),
),
∴顶点在函数y=x﹣1上;
(3)由(1)、(2)可得,该抛物线与x轴的一个交点为(1,0),对称轴为直线x=1﹣![]() .
.
①

当m>0时,抛物线开口方向向上,且1﹣![]() <1,
<1,
由图象可知,要满足条件,只要x=0式,y=m﹣2>0,
∴m>2;
②
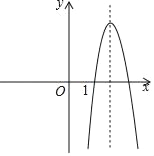
当m<0时,抛物线开口方向向下,且1﹣![]() >1,
>1,
由图象可知,不符合题意;
综上所述,m的取值范围是:m>2.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目