题目内容
【题目】如图，在平面直角坐标系中， 
， 
两点的坐标分别为
， 
，连接
，若以点
， 
， 
为顶点的三角形是等腰直角三角形，则点
坐标为__________．
【答案】
， 
， 
， 
， 
， 
【解析】∵A、B两点的坐标分别为（-4，0）、（0，2）
∴OA=4，OB=2.
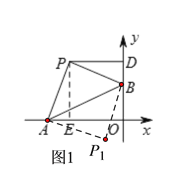
（1）如图，当∠APB=90°时，作PE⊥OA于点E，
易证△APE≌△BPD，则PD=PE=OE=OD，AE=BD，
设PD= 
，
则
，解得： 
，
∴此时点P的坐标为（-3，3）；
同理可得：点P1的坐标为（-1，-1）.
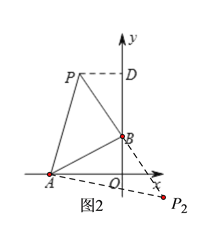
（2）如图2，当∠ABP=90°时，作PD⊥OB于点D，
易证△ABO≌△BPD，则PD=OB=2，BD=AO=4，
∴OD=OB+BD=6，
∴点P的坐标为（-2，6）.
同理可得P2的坐标为（2，-2）.
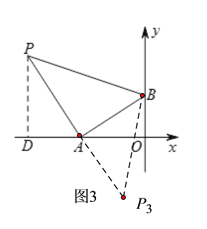
（3）如图3，过点P作PD⊥OA于点D，
易证△PDA≌△AOB，则AD=BO=2，PD=AO=4，
∴OD=AD+OA=6，
∴点P的坐标为（-6，4）.
同理可得点P3的坐标为（-2，-4）.
综上所述，若△PAB为等腰直角三角形，则点P的坐标为：（-3，3）、（-1，-1）、（-2，6）、（2，-2）、（-6，4）和（-2，-4）.
练习册系列答案
阅读快车系列答案
相关题目
