题目内容
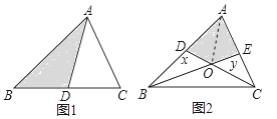
【题目】如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.

试证: ![]() =
=![]() .
.
【答案】证明见解析
【解析】试题分析:根据等腰三角形的性质由OC=OD得∠OCD=∠ODC,由OA=OB得∠A=∠B,再根据三角形外角性质得∠OCD=∠A+∠AOC,∠ODC=∠B+∠BOD,利用等量代换得到∠AOC=∠BOD,然后根据在同圆和等圆中,相等的圆心角所对的弧相等即可得到结论.
证明:∵OC=OD,∴∠OCD=∠ODC.
∵AO=OB,∴∠A=∠B.
∴∠OCD-∠A=∠ODC-∠B,
即∠AOC=∠BOD,
即∠AOE=∠BOF.∴![]() =
=![]() .
.
点睛:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目