题目内容
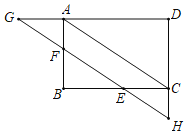
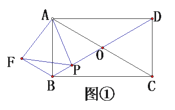
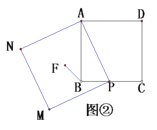
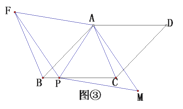
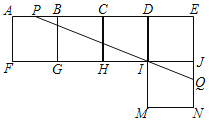
【题目】如图,一“L”型纸片是由5个边长都是10cm的正方形拼接而成,过点I的直线分别与AE,JN交于点P,Q,且“L”型纸片被直线PQ分成面积相等的上下两部分,将该纸片沿BG,CH,DI,IJ折成一个无盖的正方体盒子后,点P,Q之间的距离为_____cm.
【答案】10
【解析】
首先证明PB+QJ=10,在立体图形中,证明四边形BGQP为矩形,根据矩形的性质解答即可.
解:平面图形中,∵IJ∥PE,
∴△QIJ∽△QPE,
![]()
![]() ,即
,即![]() ,
,
∴10EQ+10PE=PEEQ,
∵图L被直线PQ分成面积相等的上、下两部分,
![]()
![]() ,
,
∴PEQE=500,即PE+QE=50(cm),
∴PB+JQ=50﹣40=10(cm),
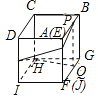
立体图形中,连接MN,
∵PB+JQ=10,JQ+QG=10,
∴PB=QG,
∴四边形BGQP为矩形,
∴PQ=BG=10(cm),
故答案为10.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
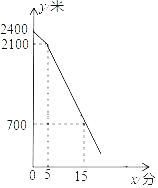
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于