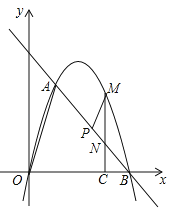题目内容
【题目】如图，在平面直角坐标系xOy中，抛物线
与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C（0，
），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．
（1）求a的值及点A，B的坐标；
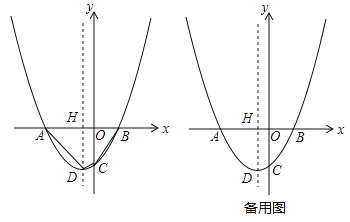
（2）当直线l将四边形ABCD分为面积比为3：7的两部分时，求直线l的函数表达式；
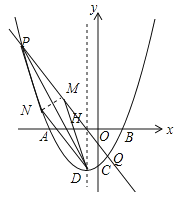
（3）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．
【答案】（1）
，A（－4，0），B（2，0）；（2）y＝2x＋2或
；（3）存在，N（－
， 1）．
【解析】
试题分析：（1）把点C代入抛物线解析式即可求出a，令y=0，列方程即可求出点A、B坐标．
（2）先求出四边形ABCD面积，分两种情形：①当直线l边AD相交与点M1时，根据S△AHM1＝
×10＝3，求出点M1坐标即可解决问题．②当直线l边BC相交与点M2时，同理可得点M2坐标．
（3）设P（
，
）、Q（
，
）且过点H（﹣1，0）的直线PQ的解析式为y=kx+b，得到b=k，利用方程组求出点M坐标，求出直线DN解析式，再利用方程组求出点N坐标，列出方程求出k，即可解决问题．
试题解析：（1）∵抛物线与y轴交于点C（0，
），∴a﹣3=，解得：，∴
当y=0时，有
，∴ 
，
，∴A（﹣4，0），B（2，0）．
（2）∵A（﹣4，0），B（2，0），C（0，），D（﹣1，﹣3）
∴S四边形ABCD=S△ADH+S梯形OCDH+S△BOC=
=10．
从面积分析知，直线l只能与边AD或BC相交，所以有两种情况：
①当直线l边AD相交与点M1时，则S△AHM1＝×10＝3，∴
×3×（－yM1）＝3，∴yM1＝－2，点M1（﹣2，﹣2），过点H（﹣1，0）和M1（﹣2，﹣2）的直线l的解析式为y=2x+2．
②当直线l边BC相交与点M2时，同理可得点M2（，﹣2），过点H（﹣1，0）和M2（，﹣2）的直线l的解析式为．
综上所述：直线l的函数表达式为y=2x+2或．
（3）设P（，）、Q（，）且过点H（﹣1，0）的直线PQ的解析式为y=kx+b，∴﹣k+b=0，∴b=k，∴y=kx+k．
由
，∴
，∴
，
，∵点M是线段PQ的中点，∴由中点坐标公式的点M（
，
）．
假设存在这样的N点如图，直线DN∥PQ，设直线DN的解析式为y=kx+k﹣3，由
，解得：
， 
， ∴N（
，
）．
∵四边形DMPN是菱形，∴DN=DM，∴
，整理得：
，
，∵ 
＞0，∴
，解得
，∵k＜0，∴
，∴P（－
，6），M（－
，2），N（－， 1），∴PM=DN=
，∵PM∥DN，∴四边形DMPN是平行四边形，∵DM=DN，∴四边形DMPN为菱形，∴以DP为对角线的四边形DMPN能成为菱形，此时点N的坐标为（﹣，1）．
