题目内容
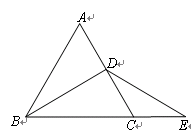
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
(1)试说明BD=DF;
(2)请写出图中所有的等腰三角形;
(3)线段BD,CE,DE之间存在怎样的数量关系?请说明理由.

(1)试说明BD=DF;
(2)请写出图中所有的等腰三角形;
(3)线段BD,CE,DE之间存在怎样的数量关系?请说明理由.
(1)∵BF平分∠ABC ∴∠ABF﹦∠CBF
∵DF∥BC ∴∠BFD﹦∠CBF ∴∠ABF﹦∠BFD ∴BD=DF …4分
(2)ΔBDF,ΔCEF …8分
(3)BD=CE+DE …9分 理由:由(1)知BD=DF,同理CE=EF
∵DF=DE+EF ∴BD=CE+DE …12分
∵DF∥BC ∴∠BFD﹦∠CBF ∴∠ABF﹦∠BFD ∴BD=DF …4分
(2)ΔBDF,ΔCEF …8分
(3)BD=CE+DE …9分 理由:由(1)知BD=DF,同理CE=EF
∵DF=DE+EF ∴BD=CE+DE …12分
(1)根据角平分线和平行线的性质求证
(2)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(3)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE.
(2)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(3)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE.

练习册系列答案
相关题目
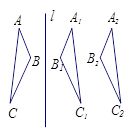
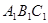 与△ABC关于直线
与△ABC关于直线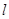 对称,将△
对称,将△ ,由此得到下列判断:①AB∥
,由此得到下列判断:①AB∥ ;②∠A=∠
;②∠A=∠ ;③AB=
;③AB=