题目内容
在平面直角坐标系xOy中,抛物线y1=2x2+
的顶点为M,直线y2=x,点P(n,0)为x轴上的一个动点,过点P作x轴的垂线分别交抛物线y1=2x2+
和直线y2=x于点A,点B.
(1)直接写出A,B两点的坐标(用含n的代数式表示);
(2)设线段AB的长为d,求d关于n的函数关系式及d的最小值,并直接写出此时线段OB与线段PM的位置关系和数量关系;
(3)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+
,求a,b,c的值.
| 1 |
| 4 |
| 1 |
| 4 |
(1)直接写出A,B两点的坐标(用含n的代数式表示);
(2)设线段AB的长为d,求d关于n的函数关系式及d的最小值,并直接写出此时线段OB与线段PM的位置关系和数量关系;
(3)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+
| 1 |
| 4 |
(1)当x=n时,y1=2n2+
,y2=n;
∴A(n,2n2+
),B(n,n).
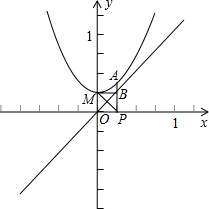 (2)d=AB=|yA-yB|=|2n2-n+
(2)d=AB=|yA-yB|=|2n2-n+
|.
∴d=|2(n-
)2+
|=2(n-
)2+
.
∴当n=
时,d取得最小值
.
此时,B(
,
),而M(0,
)、P(
,0)
∴四边形OMBP是正方形
∴当d取最小值时,线段OB与线段PM的位置关系和数量关系是OB⊥PM且OB=PM.(如图)
(3)∵对一切实数x恒有x≤y≤2x2+
,
∴对一切实数x,x≤ax2+bx+c≤2x2+
都成立.(a≠0)①
当x=0时,①式化为0≤c≤
.
∴整数c的值为0.
此时,对一切实数x,x≤ax2+bx≤2x2+
都成立.(a≠0)
即
对一切实数x均成立.
由②得ax2+(b-1)x≥0(a≠0)对一切实数x均成立.
∴
由⑤得整数b的值为1.
此时由③式得,ax2+x≤2x2+
对一切实数x均成立.(a≠0)
即(2-a)x2-x+
≥0对一切实数x均成立.(a≠0)
当a=2时,此不等式化为-x+
≥0,不满足对一切实数x均成立.
当a≠2时,∵(2-a)x2-x+
≥0对一切实数x均成立,(a≠0)
∴
∴由④,⑥,⑦得0<a≤1.
∴整数a的值为1.
∴整数a,b,c的值分别为a=1,b=1,c=0.
| 1 |
| 4 |
∴A(n,2n2+
| 1 |
| 4 |
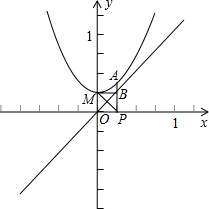 (2)d=AB=|yA-yB|=|2n2-n+
(2)d=AB=|yA-yB|=|2n2-n+| 1 |
| 4 |
∴d=|2(n-
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
∴当n=
| 1 |
| 4 |
| 1 |
| 8 |
此时,B(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴四边形OMBP是正方形
∴当d取最小值时,线段OB与线段PM的位置关系和数量关系是OB⊥PM且OB=PM.(如图)
(3)∵对一切实数x恒有x≤y≤2x2+
| 1 |
| 4 |
∴对一切实数x,x≤ax2+bx+c≤2x2+
| 1 |
| 4 |
当x=0时,①式化为0≤c≤
| 1 |
| 4 |
∴整数c的值为0.
此时,对一切实数x,x≤ax2+bx≤2x2+
| 1 |
| 4 |
即
|
由②得ax2+(b-1)x≥0(a≠0)对一切实数x均成立.
∴
|
由⑤得整数b的值为1.
此时由③式得,ax2+x≤2x2+
| 1 |
| 4 |
即(2-a)x2-x+
| 1 |
| 4 |
当a=2时,此不等式化为-x+
| 1 |
| 4 |
当a≠2时,∵(2-a)x2-x+
| 1 |
| 4 |
∴
|
∴由④,⑥,⑦得0<a≤1.
∴整数a的值为1.
∴整数a,b,c的值分别为a=1,b=1,c=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 为A(-1,0),C(0,-3).
为A(-1,0),C(0,-3).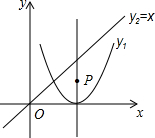

 在,请说明理由;
在,请说明理由;