题目内容

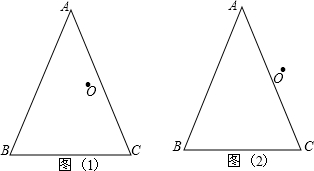
已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q.

(1)若四边形ABCD如图19-1-16所示，判断下列结论是否正确.(正确的在括号里填“√”，错误的在括号里填“×”)

甲：顺次连接EF、FG、GH、HE一定会得到平行四边形.(　　)

乙：顺次连接EQ、QG、GP、PE一定会得到平行四边形.(　　)

(2)请选择甲、乙中的一个，证明你对它的判断.

(3)若四边形ABCD如图19-1-17所示，请你判断(1)中的两个结论是否成立?

　　　　　 　　　　

图19-1-16　　　　　　　　　　 图19-1-17
答案：
解析：

 思路解析：利用三角形中位线定理和平行四边形的判定定理进行判断.

答案：(1)甲“√”，乙“×”.∵当AD∥BC时，EQ、PG为一条直线.

(2)选择甲，因为E、F分别是AB、BC的中点，所以EF∥AC，EF=AC.

同理，GH∥AC，GH=AC.

所以EFHC.

所以四边形EFGH是平行四边形.

(3)甲、乙都成立.


练习册系列答案
相关题目
已知平行四边形ABCD，AD=a，AB=b，∠ABC=α．点F为线段BC上一点（端点B，C除外），连接AF，AC精英家教网，连接DF，并延长DF交AB的延长线于点E，连接CE．
（1）当F为BC的中点时，求证：△EFC与△ABF的面积相等；
（2）当F为BC上任意一点时，△EFC与△ABF的面积还相等吗？说明理由．
在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
（1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
（2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
（3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）
精英家教网
已知，在△ABC中，AB=AC，在图（1）中，点O是△ABC内的任意一点，而在图（2）中，点O是△ABC外的任意一点．在两图中，分别以OB，OC为边画出平行四边形OBDC，连接并延长OA到E，使得AE=OA，再连接DE．观察两图，写出与线段DE有关的两个猜想，并在其中的一个图形中给出证明．（要求：在猜想中不能出现已知中未标的字母．）
精英家教网
（2012•浦口区一模）提出问题：
如图，在△ABC中，∠A=90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接EG，小亮发现△ABC与△AEG面积相等．小亮思考：这个问题中，如果∠A≠90°，那么△ABC与△AEG面积是否仍然相等？
猜想结论：
经过研究，小亮认为：上述问题中，对于任意△ABC，分别以边AB、AC向外作正方形ABDE 和正方形 ACFG，连接EG，那么△ABC与△AEG面积相等．
证明猜想：
（1）请你帮助小亮画出图形，并完成证明过程．已知：以△ABC的两边AB、AC为边长分别向外作正方形ABDE、ACFG，连接GE．求证：S△AEG=S△ABC．
结论应用：
（2）学校教学楼前的一个六边形花圃被分成七个部分，分别种上不同品种的花卉，其中四边形ABCD、CIHG、GFED均为正方形，且面积分别为9m2、5m2和4m2．求这个六边形花圃ABIHFE的面积．
已知：在△ABC中，AB=AC=5，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求证：四边形AQMP是平行四边形．
（2）求四边形AQMP的周长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网