题目内容
 (2012•浦口区一模)提出问题:
(2012•浦口区一模)提出问题:如图,在△ABC中,∠A=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接EG,小亮发现△ABC与△AEG面积相等.小亮思考:这个问题中,如果∠A≠90°,那么△ABC与△AEG面积是否仍然相等?
猜想结论:
经过研究,小亮认为:上述问题中,对于任意△ABC,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,那么△ABC与△AEG面积相等.
证明猜想:
(1)请你帮助小亮画出图形,并完成证明过程.已知:以△ABC的两边AB、AC为边长分别向外作正方形
 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.结论应用:
(2)学校教学楼前的一个六边形花圃被分成七个部分,分别种上不同品种的花卉,其中四边形ABCD、CIHG、GFED均为正方形,且面积分别为9m2、5m2和4m2.求这个六边形花圃ABIHFE的面积.
分析:(1)分为3种情况,当∠BAC=90°时,根据正方形的性质证明三角形全等就可以得出结论;当∠BAC<90°时,过C作CM⊥AB,垂足为M,过G作GN⊥AE,与AE的延长线交于点N.同样证明三角形全等可以得出结论;当∠BAC>90°时,通过作辅助线BM⊥CG的延长线与M,EN⊥AG于N,通过证明△BMA≌△ENA同样可以得出结论.
(2)先由条件根据勾股定的逆定理可以求出△DCG是直角三角形,可以求出△DCG的面积,根据(1)的结论就可以知道△ADE、△FGH△、△CBI均与△DCG的面积相等,从而就可以求出六边形的面积.
(2)先由条件根据勾股定的逆定理可以求出△DCG是直角三角形,可以求出△DCG的面积,根据(1)的结论就可以知道△ADE、△FGH△、△CBI均与△DCG的面积相等,从而就可以求出六边形的面积.
解答:(1)证明:①如图(1),当∠BAC=90°时,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=90°,
∴∠BAC=∠EAG=90°,
∵在△BAC和△EAG中
,
∴△BAC≌△EAG(SAS),
∴S△AEG=S△ABC.
②如图(2),当∠BAC<90°时,过C作CM⊥AB,垂足为M,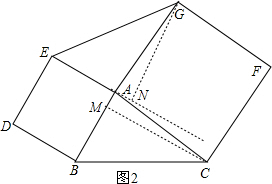
过G作GN⊥AE,与AE的延长线交于点N.
∴∠AMC=∠ANG=90°
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=90°,
∵∠GAN+∠NAC=∠GAC=90°,∠MAC+∠NAC=∠MAN=90°,
∴∠GAN=∠MAC.
∵在△GAN和△CAM中,
 ,
,
∴△AMC≌△ANG(AAS),
∴GN=CM.
∵S△AEG=
AE•GN,S△ABC=
AB•CM,
∴S△AEG=S△ABC.
③如图(3),当∠BAC>90°时,BM⊥CG的延长线与M,EN⊥AG于N,
∴∠AMB=∠ANE=90°,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=∠GAM=90°,
∴∠BAM=∠EAN.
∵在△BAM和△EAN中,
,
∴△BAM≌△EAN(AAS),
∴BM=EN.
∵S△AEG=
AG•EN,S△ABC=
AC•BM,
∴S△AEG=S△ABC.
(2)解:∵正方形ABCD、CIHG、GFED的面积分别为9m2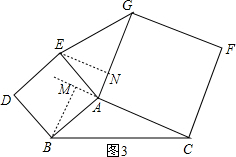 、5m2和4m2,
、5m2和4m2,
∴DC2=9m2,CG2=5m2,DG2=4m2.
∴DC2=CG2+DG2,
∴△DCG是直角三角形,
∴∠DGC=90°.
∴S△DCG=
•DG•CG=
×2×
=
m.
∵四边形ABCD、CIHG、GFED均为正方形,根据上面结论可得:
△ADE、△FGH△、△CBI均与△DCG的面积相等,
∴六边形ABIHFE的面积为9+5+4+4×
=(18+4
) m2.

∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=90°,
∴∠BAC=∠EAG=90°,
∵在△BAC和△EAG中
|
∴△BAC≌△EAG(SAS),
∴S△AEG=S△ABC.
②如图(2),当∠BAC<90°时,过C作CM⊥AB,垂足为M,

过G作GN⊥AE,与AE的延长线交于点N.
∴∠AMC=∠ANG=90°
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=90°,
∵∠GAN+∠NAC=∠GAC=90°,∠MAC+∠NAC=∠MAN=90°,
∴∠GAN=∠MAC.
∵在△GAN和△CAM中,
|
 ,
,∴△AMC≌△ANG(AAS),
∴GN=CM.
∵S△AEG=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AEG=S△ABC.
③如图(3),当∠BAC>90°时,BM⊥CG的延长线与M,EN⊥AG于N,
∴∠AMB=∠ANE=90°,
∵四边形ABDE和四边形ACFG是正方形,
∴AB=AE,AG=AC,∠BAE=∠CAG=∠GAM=90°,
∴∠BAM=∠EAN.
∵在△BAM和△EAN中,
|
∴△BAM≌△EAN(AAS),
∴BM=EN.
∵S△AEG=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AEG=S△ABC.
(2)解:∵正方形ABCD、CIHG、GFED的面积分别为9m2
 、5m2和4m2,
、5m2和4m2,∴DC2=9m2,CG2=5m2,DG2=4m2.
∴DC2=CG2+DG2,
∴△DCG是直角三角形,
∴∠DGC=90°.
∴S△DCG=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∵四边形ABCD、CIHG、GFED均为正方形,根据上面结论可得:
△ADE、△FGH△、△CBI均与△DCG的面积相等,
∴六边形ABIHFE的面积为9+5+4+4×
| 5 |
| 5 |
点评:本题考查了直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理及勾股定理的逆定理的运用,三角形面积公式的运用及正方形的性质的运用,解答时通过作辅助线证明三角形全等是关键.

练习册系列答案
相关题目
 (2012•浦口区一模)如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
(2012•浦口区一模)如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( ) (2012•浦口区一模)如图,在等腰梯形ABCD中,AE是梯形的高,将△ABE沿BC方向平移,使点A与点D重合,得△DFG.若∠B=60°,当四边形ABFD是菱形时,
(2012•浦口区一模)如图,在等腰梯形ABCD中,AE是梯形的高,将△ABE沿BC方向平移,使点A与点D重合,得△DFG.若∠B=60°,当四边形ABFD是菱形时,

 (2012•浦口区一模)一辆货车从A地出发以每小时100km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶1.8小时后,在距B地120km处与轿车相遇.图中线段表示货车离B地的距离y1与所用时间x的关系.根据函数图象探究:
(2012•浦口区一模)一辆货车从A地出发以每小时100km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶1.8小时后,在距B地120km处与轿车相遇.图中线段表示货车离B地的距离y1与所用时间x的关系.根据函数图象探究: