题目内容
设a2+2a-1=0,b4-2b2-1=0,且1-ab2≠0,求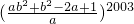 的值.
的值.
解法一:
解:∵a2+2a-1=0,b4-2b2-1=0
∴(a2+2a-1)-(b4-2b2-1)=0
化简之后得到:(a+b2)(a-b2+2)=0
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0
因此a+b2=0,即b2=-a
∴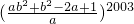 =
= =
= =(-1)2003=-1
=(-1)2003=-1
解法二:
解:a2+2a-1=0(已知),解得a=-1+ 或a=-1-
或a=-1- ,
,
由b4-2b2-1=0,解得:b2= +1,
+1,
∴ =b2+
=b2+ -2+
-2+
= +1-2+
+1-2+ ,
,
当a= -1时,原式=
-1时,原式= +1-2+4+3
+1-2+4+3 =4
=4 +3,
+3,
∵1-ab2≠0,∴a= -1舍去;
-1舍去;
当a=- -1时,原式=
-1时,原式= +1-2-
+1-2- =-1,
=-1,
∴(-1)2003=-1,
即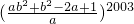 =-1.
=-1.
分析:解法一:根据1-ab2≠0的题设条件求得b2=-a,代入所求的分式化简求值.
解法二:根据a2+2a-1=0,解得a=-1+ 或a=-1-
或a=-1- ,由b4-2b2-1=0,解得:b2=
,由b4-2b2-1=0,解得:b2= +1,把所求的分式化简后即可求解.
+1,把所求的分式化简后即可求解.
点评:本题考查了因式分解、根与系数的关系及根的判别式,解题关键是注意1-ab2≠0的运用.
解:∵a2+2a-1=0,b4-2b2-1=0
∴(a2+2a-1)-(b4-2b2-1)=0
化简之后得到:(a+b2)(a-b2+2)=0
若a-b2+2=0,即b2=a+2,则1-ab2=1-a(a+2)=1-a2-2a=0,与题设矛盾,所以a-b2+2≠0
因此a+b2=0,即b2=-a
∴
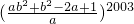 =
= =
= =(-1)2003=-1
=(-1)2003=-1解法二:
解:a2+2a-1=0(已知),解得a=-1+
 或a=-1-
或a=-1- ,
,由b4-2b2-1=0,解得:b2=
 +1,
+1,∴
 =b2+
=b2+ -2+
-2+
=
 +1-2+
+1-2+ ,
,当a=
 -1时,原式=
-1时,原式= +1-2+4+3
+1-2+4+3 =4
=4 +3,
+3,∵1-ab2≠0,∴a=
 -1舍去;
-1舍去;当a=-
 -1时,原式=
-1时,原式= +1-2-
+1-2- =-1,
=-1,∴(-1)2003=-1,
即
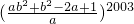 =-1.
=-1.分析:解法一:根据1-ab2≠0的题设条件求得b2=-a,代入所求的分式化简求值.
解法二:根据a2+2a-1=0,解得a=-1+
 或a=-1-
或a=-1- ,由b4-2b2-1=0,解得:b2=
,由b4-2b2-1=0,解得:b2= +1,把所求的分式化简后即可求解.
+1,把所求的分式化简后即可求解.点评:本题考查了因式分解、根与系数的关系及根的判别式,解题关键是注意1-ab2≠0的运用.

练习册系列答案
相关题目
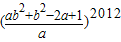 = .
= .