Question

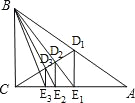
【题目】如图，已知Rt△ABC，D1是斜边AB的中点，过D1作D1E1⊥AC于E1，连接BE1交CD1于D2；过D2作D2E2⊥AC于E2，连接BE2交CD1于D3；过D3作D3E3⊥AC于E3，…，如此继续，可以依次得到点E4、E5、…、En，分别记△BCE1、△BCE2、△BCE3…△BCEn的面积为S1、S2、S3、…Sn．则Sn= S△ABC（用含n的代数式表示）．

Answer 1

【答案】.

【解析】

试题解析：易知D1E1∥BC，∴△BD1E1与△CD1E1同底同高，面积相等，以此类推；

根据直角三角形的性质以及相似三角形的性质可知：D1E1=BC，CE1=AC，S1=BCCE1=BC×AC=×ACBC=S△ABC；

∴在△ACB中，D2为其重心，

∴D2E1=BE1，

∴D2E2=BC，CE2=AC，S2=××ACBC=S△ABC，

∴D3E3=BC，CE2=AC，S3=S△ABC…；

∴Sn=S△ABC．