题目内容
【题目】解答
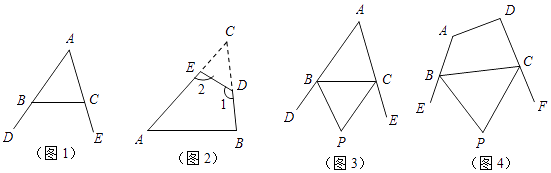
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论. 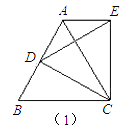
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由. 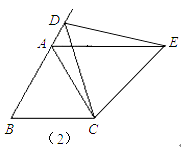
【答案】
(1)解:结论:AC=AD+AE,
证明如下:
∵△ABC、△CDE为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ECA+∠ACD=∠ACD+∠BCD,
∴∠ECA=∠BCD,
在△ACE和△BCD中
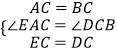
∴△ACE≌△BCD(SAS),
∴AE=BD,
∴AC=AB=AD+BD=AD+AE
(2)解:结论:AC=AE﹣AD,
理由如下:
同(1)可证明△ACE≌△BCD,
∴AE=BD,
∴AC=AB=BD﹣AD=AE﹣AD
【解析】(1)利用条件可证明△ACE≌△BCD,则可得到AE=BE,再利用线段的和差可证得结论AC=AD+AE;(2)由条件可证明△ACE≌△BCD,同样可以得到结论AC=AE﹣AD.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.

【题目】某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例计算总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(1)笔试成绩的平均数是 ;
(2)写出说课成绩的中位数为 ,众数为 ;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你通过计算判断哪两位选手将被录用?