题目内容
某水果批发市场规定,批发水果不少于100千克时,批发价为每千克2.5元.小王携带现金300元到该市场采购苹果,并以批发价买进,如果购买的苹果的质量为x千克,小王付款后的剩余现金为y元.
(1)写出y与x之间的函数关系式,并指出自变量的取值范围;
(2)画出相应的函数图象.
(1)写出y与x之间的函数关系式,并指出自变量的取值范围;
(2)画出相应的函数图象.
分析:利用已知批发价为每千克2.5元,小王携带现金3000元到这个市场采购苹果,求的解析式,又因为批发苹果不少于100千克时,批发价为每千克2.5元,所以x≥100kg.
(2)根据(1)中一次函数解析式,利用“两点确定一条直线”作出图象,注意x的取值范围.
(2)根据(1)中一次函数解析式,利用“两点确定一条直线”作出图象,注意x的取值范围.
解答:解:(1)由已知批发价为每千克2.5元,小王携带现金300元到这个市场采购苹果得y与x的函数关系式:y=300-2.5x,
∵批发苹果不少于100千克时,批发价为每千克2.5元,
∴x≥100kg,
∴至多可以买300÷2.5=120kg.
故自变量x的取值范围:100≤x≤120;
综上所述,y与x之间的函数关系式为:y=300-2.5x(100≤x≤120);
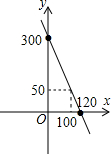
(2)由(1)知,y=300-2.5x(100≤x≤120).
令x=0,则y=300;令y=0,则x=120,
所以该直线经过点(0,300),(120,0),其图象如图所示:
∵批发苹果不少于100千克时,批发价为每千克2.5元,
∴x≥100kg,
∴至多可以买300÷2.5=120kg.
故自变量x的取值范围:100≤x≤120;
综上所述,y与x之间的函数关系式为:y=300-2.5x(100≤x≤120);
(2)由(1)知,y=300-2.5x(100≤x≤120).
令x=0,则y=300;令y=0,则x=120,
所以该直线经过点(0,300),(120,0),其图象如图所示:

点评:本题考查了一次函数的应用.利用一次函数性质,解决实际问题,把复杂的实际问题转换为数学问题.

练习册系列答案
相关题目