题目内容
【题目】如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
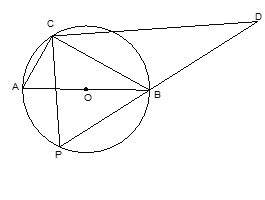
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】(1)由题意,AB是⊙O的直径;∴∠ACB=90。,∵CD⊥CP,∴∠PCD=90。
∴∠ACP+∠BCD=∠PCB+∠DCB=90。,∴∠ACP=∠DCB,又∵∠CBP=∠D+∠DCB,∠CBP=∠ABP+∠ABC,∴∠ABC=∠APC,∴∠APC=∠D,∴△PCA∽△DCB;∴![]() ,∴AC·CD=PC·BC
,∴AC·CD=PC·BC
(2)当P运动到AB弧的中点时,连接AP,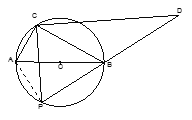
∵AB是⊙O的直径,∴∠APB=90。,又∵P是弧AB的中点,∴弧PA=弧PB,∴AP=BP,∴∠PAB=∠PBA=45.,又AB=5,∴PA=![]() ,过A作AM⊥CP,垂足为M,在Rt△AMC中,∠ACM=45,∴∠CAM=45,∴AM=CM=
,过A作AM⊥CP,垂足为M,在Rt△AMC中,∠ACM=45,∴∠CAM=45,∴AM=CM=![]() ,在Rt△AMP中,AM2+AP2=PM2,∴PM=
,在Rt△AMP中,AM2+AP2=PM2,∴PM=![]() ,∴PC=PM+
,∴PC=PM+![]() =
=![]() 。由(1)知:AC·CD=PC·BC ,3×CD=PC×4,∴CD=
。由(1)知:AC·CD=PC·BC ,3×CD=PC×4,∴CD=![]()
(3)由(1)知:AC·CD=PC·BC,所以AC:BC=CP:CD;
所以CP:CD=3:4,而△PCD的面积等于![]() ·
·![]() =
=![]() ,
,
CP是圆O的弦,当CP最长时,△PCD的面积最大,而此时C
P就是圆O的直径;所以CP=5,∴3:4=5:CD;
∴CD=![]() ,△PCD的面积等于
,△PCD的面积等于![]() ·
·![]() =
=![]() =
=![]() ;
;
(1)通过求证△PCA∽△DCB,即可求证AC·CD=PC·BC
(2)当P运动到AB弧的中点时,连接AP,求出PA,过A作AM⊥CP,垂足为M,求出AM,
从而求出PC ,由(1)可知CD的长
(3)当CP最长时,即为圆的直径,△PCD的面积最大,由(1)可求得CD的长,从而求出△PCD的面积

 名校课堂系列答案
名校课堂系列答案