题目内容
已知关于x的一元二次方程(m2-1)x2-6(3m-1)x+72=0.
(1)若x=1是这个方程的一个根,求m的值和方程的另一个根;
(2)求m是什么整数时,此方程有两个不相等的正实数根?
解:(1)设方程的另一根为a,
∵x=1是这个方程的一个根,
∴(m2-1)-6(3m-1)+72=0.
整理得:m2-18m+77=0.
解得:m=11或7,
∵1×a= ,
,
解得a= 或a=
或a= .
.
(2)∵m2-1≠0
∴m≠±1
∵△=36(m-3)2>0
∴m≠3
用求根公式可得:x1=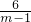 ,x2=
,x2=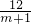
∵x1,x2是正整数
∴m-1=1,2,3,6,m+1=1,2,3,4,6,12,
解得m=2.
分析:(1)把x=1代入方程求出a的值,再把a的值代入方程,求出方程的另一个根;
(2)首先根据已知条件可得m2-1≠0,进而得到m≠±1,然后根据根的判别式△>0,可得m≠3;再利用求根公式用含m的式子表示x,因为,方程有两个不相等的正整数根,所以分情况讨论m的值即可.
点评:此题主要考查了一元二次方程的二次项系数不能为0,根的判别式和求方程的整数解的综合运用,还用到了数学中的分类讨论思想,综合性较强.
∵x=1是这个方程的一个根,
∴(m2-1)-6(3m-1)+72=0.
整理得:m2-18m+77=0.
解得:m=11或7,
∵1×a=
 ,
,解得a=
 或a=
或a= .
.(2)∵m2-1≠0
∴m≠±1
∵△=36(m-3)2>0
∴m≠3
用求根公式可得:x1=
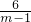 ,x2=
,x2=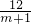
∵x1,x2是正整数
∴m-1=1,2,3,6,m+1=1,2,3,4,6,12,
解得m=2.
分析:(1)把x=1代入方程求出a的值,再把a的值代入方程,求出方程的另一个根;
(2)首先根据已知条件可得m2-1≠0,进而得到m≠±1,然后根据根的判别式△>0,可得m≠3;再利用求根公式用含m的式子表示x,因为,方程有两个不相等的正整数根,所以分情况讨论m的值即可.
点评:此题主要考查了一元二次方程的二次项系数不能为0,根的判别式和求方程的整数解的综合运用,还用到了数学中的分类讨论思想,综合性较强.

练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.