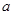题目内容
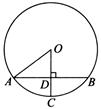
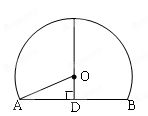
如图,⊙O的直径AB=4,C、D为圆周上两点,且四边形OBCD是菱形,过点D的直线EF∥AC,交BA、BC的延长线于点E、F.
小题1:求证:EF是⊙O的切线
小题2:求DE的长
小题1:求证:EF是⊙O的切线
小题2:求DE的长
小题1:证明:∵AB是⊙O的直径,
∴∠ACB=90°. ……… 1分
∵四边形OBCD是菱形,
∴OD//BC.
∴∠1=∠ACB=90°. ……… 2分
∵EF∥AC,
∴∠2=∠1 =90°. ……… 3分
∵OD是半径,
∴EF是⊙O的切线. ……… 4分
小题2:解:连结OC,
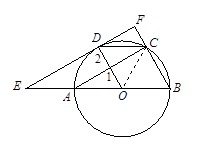
∵直径AB=4,∴半径OB=OC=2.
∵四边形OBCD是菱形,∴OD=BC=OB=OC=2.
∴∠B=60°. ……… 7分
∵OD//BC,∴∠EOD=∠B= 60°. ……… 8分
在Rt△EOD中,DE=OD•tan∠EOD=2 tan60°=2
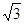 . ……… 9分
. ……… 9分 略

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 中,
中, 、
、 为
为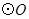 的半径,
的半径,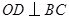 于
于 ,
,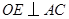 于点
于点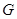 ,求证:
,求证:
 阴影部分四边形
阴影部分四边形 的面积是
的面积是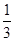 .
.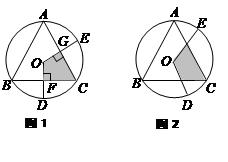
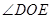 保持
保持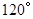 角度不变,求证:当
角度不变,求证:当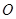 点旋转时,由两条半径
点旋转时,由两条半径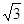
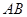 宽为10米,净
宽为10米,净 为7米,则此隧道单心圆的半径
为7米,则此隧道单心圆的半径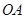 是( )
是( )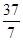
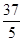
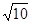 ,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则: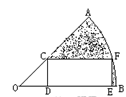
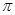 )
) 
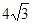 ,求图中阴影部分的面积.
,求图中阴影部分的面积.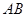 是半径为1的⊙
是半径为1的⊙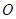 的一条弦,且
的一条弦,且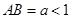 .以弦
.以弦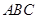 ,点
,点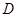 为⊙
为⊙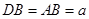 ,
,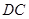 的延长线交
的延长线交 ,则
,则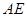 的长为( ▲ ).
的长为( ▲ ).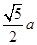 B.1 C.
B.1 C.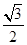 D.
D.