题目内容
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 . 
【答案】6﹣2 ![]() ≤x≤4
≤x≤4
【解析】解:如图:
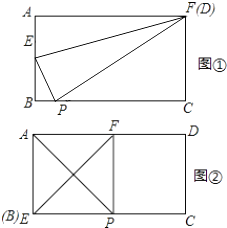
①当F、D重合时,BP的值最小;
根据折叠的性质知:AF=PF=6;
在Rt△PFC中,PF=6,FC=4,则PC=2 ![]() ;
;
∴BP=xmin=6﹣2 ![]() ;
;
②当E、B重合时,BP的值最大;根据折叠的性质即可得到AB=BP=4,即BP的最大值为4;
故答案为:6﹣2 ![]() ≤x≤4.
≤x≤4.
①当F、D重合时,BP的值最小;由折叠的性质知AF=PF=6;根据勾股定理得出PC的长,进而找到BP的最小值;②当E、B重合时,BP的值最大;根据折叠的性质即可得到AB=BP=4,即BP的最大值为4;从而找到BP的取值范围。

练习册系列答案
相关题目