Question

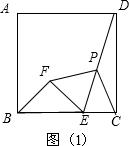
如图①，正方形ABCD中，∠FOE=90°，顶点O与D点重合，交直线BC于E，交直线BA于F．
（1）求证：OF=OE；
（2）如图②，若O点在射线BD上运动，其它条件不变，上述结论是否仍然成立？画出图形，直接写出结论；
（3）如图③，O为正方形ABCD对角线的中点，∠FOE=90°且绕点O旋转，交BC、CD边于F、E点．（1）中的结论是否仍然成立？请说明理由．

Answer 1

（1）∵∠EDC=∠FDA，∠C=∠FAD，OC=OA，
∴△OEC≌△OFA，
∴OF=OE．（3分）

（2）OF=OE仍然成立．（4分）
如图：作OH⊥AF，OG⊥EC，
根据旋转不变性可知，∠FOH=∠EOG，
易得，OH=OG，
又∵∠FHO=∠GEO，
∴△FHO≌△EGO，
∴OF=OE．（6分）

（3）作OM⊥BC于M，ON⊥CD于N，
∴∠OMF=∠ONE，OM=ON=

1

2

CD，∠MOF=∠NOE=90°-∠FON，
∴△OMF≌△ONE，
∴OF=OE．（10分）