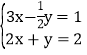题目内容
【题目】学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形。
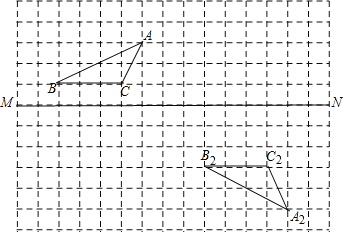
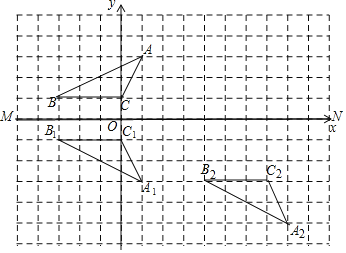
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为(a+b)的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式:______________



(2)若用图1中的8块C型长方形卡片可以拼成如图3所示的长方形,它的宽为20cm,请你求出每块长方形的面积
(3)选取1张A型卡片,3张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S2-S1,则当a与b满足_________时,S为定值,且定值为___________.

【答案】(1)a2+2ab+b2=(a+b)2;(2)75 cm2;(3)a=2b,a2-ab.
【解析】
(1)结合图形,直接由等积法可得完全平方和公式;
(2)结合图形,建立关于a,b的二元一次方程组,解方程组即可;
(3)设DG长为x,结合图形,用含x的式子分别表示出S1,S2,继而得到S的表达式,根据S为定值,与x无关,从而得到a,b的关系式及定值.
解:(1)A型卡片的面积为a2,B型卡片的面积为b2,C型卡片的面积为ab,
题中已经选择1张A型卡片,2张C型卡片,一张B型卡片,面积之和为a2+2ab+b2,由图可知,也正好拼成了一个边长为(a+b)的正方形,由此可以得到一个完全平方公式,故答案为:a2+2ab+b2=(a+b)2;
(2)由图可得关于a,b的二元一次方程
![]() ,
,
解得:![]() ,
,
S=ab=5×15=75 (cm2)
故每个C型长方形的面积为75 cm2
(3)设DG长为x,由图可知
S1=a[x-(a+b)]=ax-a2-ab
S2=2b(x-a)=2bx-2ab
S=S2-S1= 2bx-2ab-( ax-a2-ab)=(2b-a)x+a2-ab
由题意得,若S为定值,则S将不随x的变化而变化,
可知当2b-a=0时,即a=2b时,S= a2-ab为定值
故答案为:a=2b,a2-ab.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中甲、乙两组学生人数都为6人,成绩如下(单位:分):
甲:7,9,10,8,5,9;
乙:9,6,8,10,7,8
(1)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | |
甲组 | 8 | 9 | ||
乙组 |
| 8 | 8 |
(2)甲组学生说他们的众数高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出一条支持乙组学生观点的理由. .
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.