题目内容
阅读下列材料:
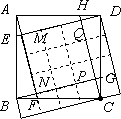
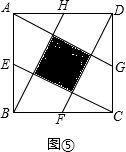
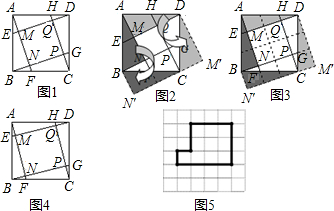
小明遇到一个问题:如图,正方形ABCD中,E、F、G、H分别是AB、BC、CD和DA边上靠近A、B、C、D的n等分点,连结AF、BG、CH、DE,形成四边形MNPQ.求四边形MNPQ与正方形ABCD的面积比(用含n的代数式表示).

小明的做法是:
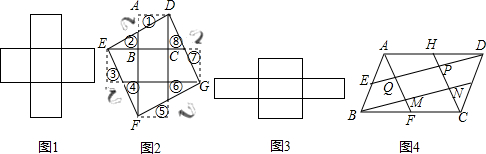
先取n=2,如图,将△ABN绕点B顺时针旋转90゜至△CB![]() ,再将△ADM绕点D逆时针旋转90°至△CD
,再将△ADM绕点D逆时针旋转90°至△CD![]() ,得到5个小正方形,所以四边形MNPQ与正方形ABCD的面积比是
,得到5个小正方形,所以四边形MNPQ与正方形ABCD的面积比是![]() ;
;
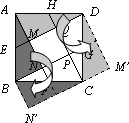
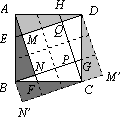
然后取n=3,如图,将△ABN绕点B顺时针旋转90°至△CB![]() ,再将△ADM绕点D逆时针旋转90°至△CD
,再将△ADM绕点D逆时针旋转90°至△CD![]() ,得到10个小正方形,所以四边形MNPQ与正方形ABCD的面积比是
,得到10个小正方形,所以四边形MNPQ与正方形ABCD的面积比是![]() ,即
,即![]() ;
;
……
请你参考小明的做法,解决下列问题:
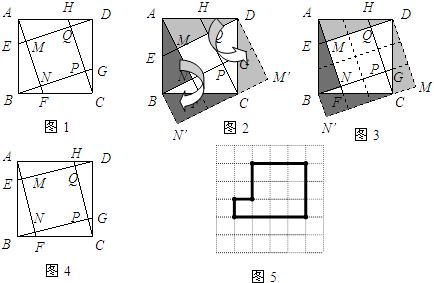
(1)在下图中探究n=4时四边形MNPQ与正方形ABCD的面积比(在图上画图并直接写出结果);

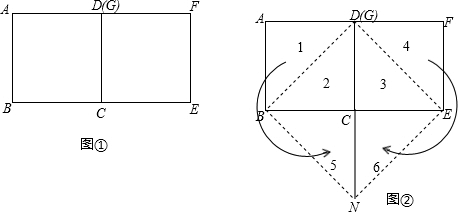
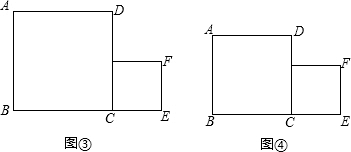
(2)下图是矩形纸片剪去一个小矩形后的示意图,请你将它剪成三块后再拼成正方形(在图中画出并指明拼接后的正方形).

答案:
解析:
解析:
|
1分
3分 四边形MNPQ与正方形ABCD的拼接后的正方形是正方形ABCD. 面积比是 4分 |

练习册系列答案
相关题目