题目内容
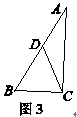
阅读下列材料:小明遇到一个问题:2个同样大小的正方形纸片排列形式如图①所示,将它们分割后拼接成一个新的正方形.
他的作法是:沿对角线剪开,按图②所示的方法,即可拼接成一个新的正方形DENB.
(1)请你参考小明的作法解决下面问题:
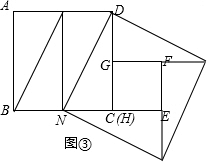
现有个边长分别为2,1的正方形纸片,排列形式如图③所示.请将其分割后拼接成一个新的正方形.要求:在图③,④中分别画出两个拼接成的新的正方形(说明:只要是符合条件的正方形即可,但要求分割方法有所不同)
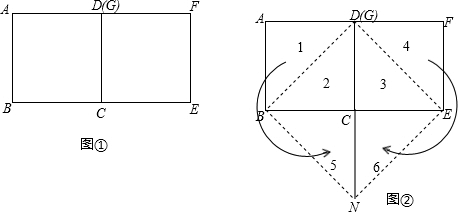
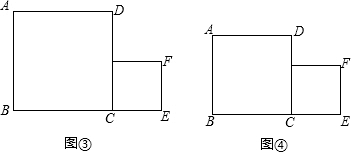
(2)求出拼接后正方形的面积;
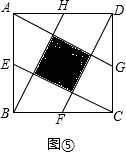
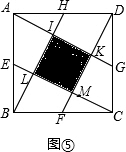
(3)如图⑤,点E、F、G、H是正方形ABCD各边的中点,要使得中间阴影部分小正方形的面积是5,那么大正方形ABCD的边长应该是多少?(直接写出结果).
分析:(1)根据题意画出图形即可;
(2)根据拼接后正方形的面积等于大正方形与小正方形的面积和进行解答即可;
(3)由小正方形的面积求出小正方形的边长,再根据点E、F、G、H是正方形ABCD各边的中点可知I、K分别为HL及DH的中点,进而可得出DK及AK的长,利用勾股定理即可求出AD的长.
(2)根据拼接后正方形的面积等于大正方形与小正方形的面积和进行解答即可;
(3)由小正方形的面积求出小正方形的边长,再根据点E、F、G、H是正方形ABCD各边的中点可知I、K分别为HL及DH的中点,进而可得出DK及AK的长,利用勾股定理即可求出AD的长.
解答:解:(1)如图所示:
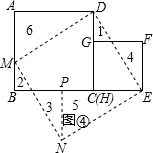
(2)∵拼接后的四边形是大正方形与小正方形的面积和,
∴其面积=2×2+1=5;
(3)∵中间阴影部分小正方形的面积是5,
∴IL=
,
∵点E、F、G、H是正方形ABCD各边的中点,
∴I、K分别为HL及DH的中点,
∴AK=2
,DK=
,
∴AD=
=
=5,即大正方形的边长是5.


(2)∵拼接后的四边形是大正方形与小正方形的面积和,
∴其面积=2×2+1=5;
(3)∵中间阴影部分小正方形的面积是5,
∴IL=
| 5 |
∵点E、F、G、H是正方形ABCD各边的中点,
∴I、K分别为HL及DH的中点,
∴AK=2
| 5 |
| 5 |
∴AD=
| AK2+DK2 |
(2
|

点评:本题考查的是作图与应用设计作图,解答此题的关键是熟知图形拼接后与原图形的面积相等.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目