��Ŀ����
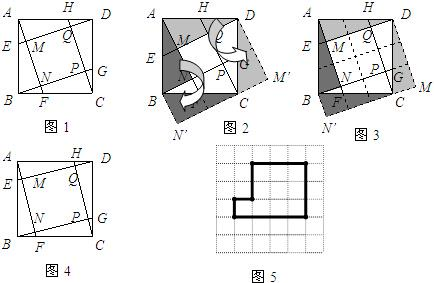
�Ķ����в��ϣ�С������һ�����⣺��ͼ1��������ABCD�У�E��F��G��H�ֱ���AB��BC��CD��DA���Ͽ���A��B��C��D��n�ȷֵ㣬����AF��BG��CH��DE���γ��ı���MNPQ�����ı���MNPQ��������ABCD������ȣ��ú�n�Ĵ���ʽ��ʾ����
С���������ǣ�
��ȡn=2����ͼ2������ABN�Ƶ�B˳ʱ����ת90�b����CBN�䣬�ٽ���ADM�Ƶ�D��ʱ����ת90�b����CDM�䣬�õ�5��С�����Σ������ı���MNPQ��������ABCD���������
| 1 | 5 |
����ο�С��������������������⣺
��1��ȡn=3����ͼ3���ı���MNPQ��������ABCD�������Ϊ
��2����ͼ4��̽����n=4ʱ�ı���MNPQ��������ABCD�������Ϊ
��3�����룺��E��F��G��H�ֱ���AB��BC��CD��DA���Ͽ���A��B��C��D��n�ȷֵ�ʱ���ı���MNPQ��������ABCD�������Ϊ
��4��ͼ5�Ǿ���ֽƬ��ȥһ��С���κ��ʾ��ͼ�����㽫�������������ƴ�������Σ���ͼ5�л�����ָ��ƴ�Ӻ�������Σ���
��������1�������ת��������εĸ�����10���м��ı����������εĸ�����4��Ȼ����㼴����⣻
��2�������ĵȷֵ����ҳ������ĵȷֵ㣬����ͼ3����������ͼ�Σ�Ȼ���ٲ����ת��������εĸ�����17���м��ı����������εĸ�����9��Ȼ����㼴����⣻
��3������ǰ�ĸ�ͼ�ε����ݹ��ɣ�������������1����ƽ������ĸ��������ƽ���ټ���1��д�����ɣ�
��4�����������10������ƴ�Ӻ�������εı߳���
��Ȼ�����������ص���м��ӣ�
��2�������ĵȷֵ����ҳ������ĵȷֵ㣬����ͼ3����������ͼ�Σ�Ȼ���ٲ����ת��������εĸ�����17���м��ı����������εĸ�����9��Ȼ����㼴����⣻
��3������ǰ�ĸ�ͼ�ε����ݹ��ɣ�������������1����ƽ������ĸ��������ƽ���ټ���1��д�����ɣ�
��4�����������10������ƴ�Ӻ�������εı߳���
| 10 |
����⣺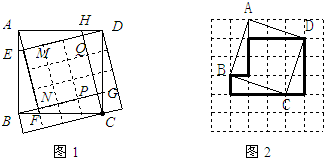 ��1��������ABCD�������10��С�����Σ��ı���MNPQ��4��С�����Σ�
��1��������ABCD�������10��С�����Σ��ı���MNPQ��4��С�����Σ�
���ı���MNPQ��������ABCD�������Ϊ��
=
����2�֣�
��2����ͼ1����3�֣�
������ABCD�������17��С�����Σ��ı���MNPQ��9��С�����Σ�
���ı���MNPQ��������ABCD�������Ϊ��
����5�֣�
��3��������ABCD�������n2+1��С�����Σ��ı���MNPQ�ǣ�n-1��2��С�����Σ�
���ı���MNPQ��������ABCD�������Ϊ��
����7�֣�
��4����ͼ2����8�֣�
��ÿ��С�����ε������1��ͼ�������10��
����ƴ�Ӻ�������εı߳���
��
��ƴ�Ӻ�������ε���������ABCD����9�֣�
 ��1��������ABCD�������10��С�����Σ��ı���MNPQ��4��С�����Σ�
��1��������ABCD�������10��С�����Σ��ı���MNPQ��4��С�����Σ����ı���MNPQ��������ABCD�������Ϊ��
| 4 |
| 10 |
| 2 |
| 5 |
��2����ͼ1����3�֣�
������ABCD�������17��С�����Σ��ı���MNPQ��9��С�����Σ�
���ı���MNPQ��������ABCD�������Ϊ��
| 9 |
| 17 |
��3��������ABCD�������n2+1��С�����Σ��ı���MNPQ�ǣ�n-1��2��С�����Σ�
���ı���MNPQ��������ABCD�������Ϊ��
| (n-1)2 |
| n2+1 |
��4����ͼ2����8�֣�
��ÿ��С�����ε������1��ͼ�������10��
����ƴ�Ӻ�������εı߳���
| 10 |
��ƴ�Ӻ�������ε���������ABCD����9�֣�
���������⿼���������ε����ʣ���ת�����ʣ��Լ������ͼ���ѶȲ�������Ŀ�ṩ����Ϣ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ