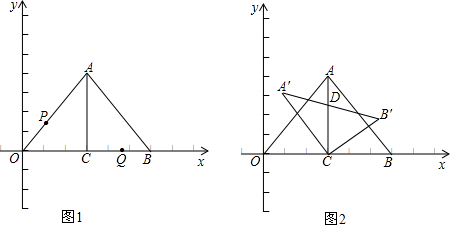题目内容
在平面直角坐标系中有一点A( ),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.(1)当B点在A点右侧时,如图(1).如果∠AOB=20°,∠A1OB=110°,α=______.这时直线AB1与直线A1B有何特殊的位置关系证明你的结论.
(2)如果B点的横坐标为t,△OAB的面积为S,直接写出S关于t的函数关式,并指出t的取值范围.
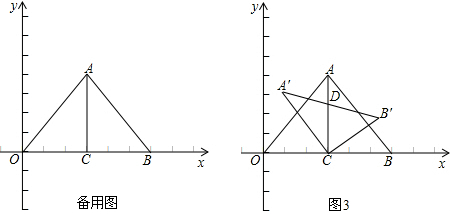
(3)当α=60时,直线B1A交y轴于D,求以D为顶点且经过A点的抛物线的解析式.

【答案】分析:(1)易知∠α=90°;
直线AB1与直线A1B可通过证△A1OB和AOB1全等得出∠AB1O=∠A1BO,因此两角加上一个相等的对顶角后也应该相等,由于∠B1OB=α=90°,因此A1B⊥AB1.
(2)已知了A的坐标和B的横坐标即可得出AB的长和AB边上的高,根据三角形的面积计算公式即可得出S,t的函数关系式.(要注意的本题中,要保证线段的长均为正数)
(3)本题要分两种情况进行求解,以B在A点右侧为例进行说明.
设直线l与y轴的交点为M,根据A的坐标不难得出∠AOM=30°,∠OAM=60°,因此当α=60°时,A1恰好在直线l上,且A1,A关于y轴对称,由此可得出A1的坐标.求抛物线的解析式关键还需知道D点的坐标,根据(1)的全等三角形可得出∠OAB1=∠OA1B=60°,因此∠AOD=∠ADO=30°,D,O关于直线l对称由此可得出D点的坐标,然后用待定系数法即可求出抛物线的解析式.
解答: 解:(1)90.垂直,理由:
解:(1)90.垂直,理由:
设AB1与OB交于C.
在△A1OB和△AOB1中,
∴△A1OB≌△AOB1
∴∠A1BO=∠AB1O.又∠AB1O+∠OCB1=90°,∠OCB1=∠ACB
∴∠ACB+∠A1BO=90°
∴B1A⊥A1B.
(2)当t> 时,S=
时,S= (t-
(t- )
)
当t< 时,S=
时,S= (t-
(t- )
)
(或x≠ 时)S=
时)S= |t-
|t- |.
|.
(3)当B在A点右侧时.如图(2)(画图)
∵A(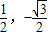 ),若l与y轴交于M.则OM=
),若l与y轴交于M.则OM=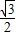 ,MA=
,MA= ,
,
∴∠AOM=30°α=60时,A1点在l上.
∴△OA1A是等边三角形.
∴∠AA1O=60度.
与(1)同理得△A1OB≌△AOB1.
∴∠OAB1=∠OA1B=60°
∴B1A∥OA1
∴D(O,-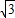 ).
).
当B在A点左侧时,同理可得B1A∥OA1,D(O,-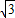 ).(可以证左侧,同理得右侧)
).(可以证左侧,同理得右侧)
因此,所求解析式为y=2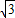 x2-
x2-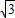 .
.
点评:本题考查了图形的旋转变换、全等三角形的判定和性质、等边三角形的判定和性质、二次函数的应用等知识点.
直线AB1与直线A1B可通过证△A1OB和AOB1全等得出∠AB1O=∠A1BO,因此两角加上一个相等的对顶角后也应该相等,由于∠B1OB=α=90°,因此A1B⊥AB1.
(2)已知了A的坐标和B的横坐标即可得出AB的长和AB边上的高,根据三角形的面积计算公式即可得出S,t的函数关系式.(要注意的本题中,要保证线段的长均为正数)
(3)本题要分两种情况进行求解,以B在A点右侧为例进行说明.
设直线l与y轴的交点为M,根据A的坐标不难得出∠AOM=30°,∠OAM=60°,因此当α=60°时,A1恰好在直线l上,且A1,A关于y轴对称,由此可得出A1的坐标.求抛物线的解析式关键还需知道D点的坐标,根据(1)的全等三角形可得出∠OAB1=∠OA1B=60°,因此∠AOD=∠ADO=30°,D,O关于直线l对称由此可得出D点的坐标,然后用待定系数法即可求出抛物线的解析式.
解答:
 解:(1)90.垂直,理由:
解:(1)90.垂直,理由:设AB1与OB交于C.
在△A1OB和△AOB1中,

∴△A1OB≌△AOB1
∴∠A1BO=∠AB1O.又∠AB1O+∠OCB1=90°,∠OCB1=∠ACB
∴∠ACB+∠A1BO=90°
∴B1A⊥A1B.
(2)当t>
 时,S=
时,S= (t-
(t- )
)当t<
 时,S=
时,S= (t-
(t- )
)(或x≠
 时)S=
时)S= |t-
|t- |.
|.(3)当B在A点右侧时.如图(2)(画图)
∵A(
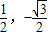 ),若l与y轴交于M.则OM=
),若l与y轴交于M.则OM=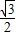 ,MA=
,MA= ,
,∴∠AOM=30°α=60时,A1点在l上.
∴△OA1A是等边三角形.
∴∠AA1O=60度.
与(1)同理得△A1OB≌△AOB1.
∴∠OAB1=∠OA1B=60°
∴B1A∥OA1
∴D(O,-
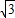 ).
).当B在A点左侧时,同理可得B1A∥OA1,D(O,-
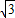 ).(可以证左侧,同理得右侧)
).(可以证左侧,同理得右侧)因此,所求解析式为y=2
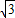 x2-
x2-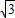 .
.点评:本题考查了图形的旋转变换、全等三角形的判定和性质、等边三角形的判定和性质、二次函数的应用等知识点.

练习册系列答案
相关题目
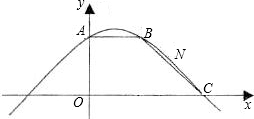 在x轴上,过A、B、C三点的抛物线表达式为
在x轴上,过A、B、C三点的抛物线表达式为