题目内容
在平面直角坐标系中有两点P(-1,1),Q (2,2),函数y=kx-1的图象与线段PQ延长线相交(交点不包括Q),则实数k的取值范围是分析:由题意可得函数过定点(0,-1),找出两临界点即可得出答案.
解答:解:函数过定点R(0,-1).可以旋转(调整斜率K),
可知临界点是与直线PQ平行,此时斜率为:k=
;
另一个临界点是RQ两点所在直线的斜率:k=
.
所以实数k的取值范围是
<k<
.
故答案为:是
<k<
.
可知临界点是与直线PQ平行,此时斜率为:k=
| 1 |
| 3 |
另一个临界点是RQ两点所在直线的斜率:k=
| 3 |
| 2 |
所以实数k的取值范围是
| 1 |
| 3 |
| 3 |
| 2 |
故答案为:是
| 1 |
| 3 |
| 3 |
| 2 |
点评:本题考查一次函数图象与系数的关系,有一定难度,关键是找出两临界条件.

练习册系列答案
相关题目
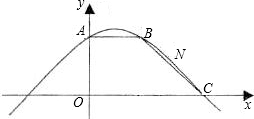 在x轴上,过A、B、C三点的抛物线表达式为
在x轴上,过A、B、C三点的抛物线表达式为